O que ondas do mar, bolhas de sabão e DNA têm em comum? É o que mostro neste artigo, com a ajuda do Python.
Nem todos têm boas lembranças das funções trigonométricas da época da escola. E, mesmo nas graduações de cursos de exatas, alguns torcem o nariz sempre que veem seno, cosseno e tangente. Neste artigo veremos como usar o SymPy para facilitar nossa vida ao encontrar funções trigonométricas (e suas “primas” também, as hiperbólicas!), além de ilustrar algumas aplicações reais de tais funções.
Tópicos
Funções trigonométricas
Apenas lembrando, as funções trigonométricas podem ser definidas como razões entre dois lados de um triângulo retângulo em função de um ângulo, ou, de forma mais geral, como razões de coordenadas de pontos no círculo unitário, ilustrado a seguir:

Círculo unitário com as coordenadas (coseno, seno) dos principais ângulos. Fonte: Wikipedia
Comecemos importando as bibliotecas que usaremos. O papel de cada uma será explicado no decorrer do artigo.
import sympy
from sympy import (sin, cos, tan, asin, acos, atan, sqrt, symbols, simplify,
trigsimp, log, exp, expand, expand_trig, Symbol, rad, deg,
sinh, cosh, tanh)
from sympy.plotting import (plot, plot3d, plot3d_parametric_line,
plot_implicit, plot3d_parametric_surface)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter, MultipleLocator
# configuração para outputs melhores no artigo, pode ser ignorado
sympy.init_printing(use_latex='png', scale=1.0, order='grlex',
forecolor='Black', backcolor='White',)Observe que importamos diretamente as funções trigonométricas do SymPy. Assim, as podemos chamar diretamente, sem precisar colocar `sympy.
sin(sympy.pi / 6)cos(sympy.pi / 6)tan(sympy.pi / 6)A mesma linha de raciocínio vale para as demais funções trigonométricas: secante (sec), cossecante (csc) e cotangente (cot).
Caso não saiba o valor em radianos para um determinado ângulo, há a função rad do SymPy:
rad(30)sin(rad(30))Também há a função deg para obter o valor em graus de um ângulo em radianos:
deg(sympy.pi / 6)Funções inversas… e cuidado com floats
As funções inversas são também chamadas de funções arco. São as famosas arco seno, arco cosseno, arco tangente… Tais funções retornam o ângulo associado a um valor. Por exemplo, sabemos que o seno de 30° é 1/2. Logo, o arco cujo seno é 1/2 é 30° ou, em radianos, π/6. Vejamos, então, o resultado de asin(1/2):
asin(1/2)Veja que o resultado não foi π/6. Ao menos não simbolicamente, o retorno foi uma aproximação numérica, um float, da divisão de pi por 6. Verifique na sua calculadora. Mas por quê? Já falamos do problema dos floats anteriormente:
1/2De forma simplificada, quando passamos 1/2 estamos passando o float 0.5 que, internamente, não necessariamente corresponde à fração 1/2. Para o SymPy entender que você realmente quer a fração 1/2 e não sua representação aproximada em float, podemos passar na forma de uma string:
asin('1/2')Agora obtivemos o resultado esperado.
Como também vimos no primeiro artigo sobre o SymPy, em uma divisão, se um dos operandos for um objeto SymPy, toda a divisão vira um objeto SymPy. Por isso que a seguinte célula retorna um fração SymPy:
acos(sympy.sqrt(3)/2)Aqui entra uma das grandes vantagens de se trabalhar simbolicamente. Lembra que quando havia uma raiz no denominador era preciso fazer um processo chamado de racionalização de denominadores? Quando passamos um objeto SymPy, ele cuida disso internamente. Veja que o resultado das duas seguintes células são iguais:
atan(1 / sympy.sqrt(3))atan(sympy.sqrt(3) / 3)Identidades trigonométricas
Parte considerável do tempo de estudo de funções trigonométricas é dedidaca ao estudo de identidades. Há uma longa lista de identidades trigonométricas e certamente não vou apresentar todas aqui. O intuito é apenas demonstrar que o SymPy reconhece identidades trigonométricas com alguns exemplos.
Comecemos criando símbolos para nossas variáveis que vão representar os ângulos:
x, y = symbols('x y')Comecemos demonstrando que o SymPy reconhece identidades referentes a ângulos complementares:
sin(x) == cos(x - sympy.pi/2)True
Agora, observe o que acontecerá na comparação a seguir, que é uma das identidades trigonométricas conhecidas como Teoremas de adição:
sin(x + y) == sin(x) * cos(y) + cos(x) * sin(y)False
Veja que o retorno foi False. Mas a identidade existe, por que não teve retorno True? Vejamos como o SymPy armazena o lado direito da comparação acima:
sin(x) * cos(y) + cos(x) * sin(y)Veja que, embora saibamos que tal soma é igual a sin(x + y), o SymPy não faz a simplificação automaticamente. Como já vimos em outro artigo, o SymPy faz comparação de forma e não de equivalência matemática. Por isso a comparação deu retorno False. Tirando casos muito simples, como a primeira comparação feita nesta seção do artigo, geralmente é recomendado comparar expressões após simplificações para ter um resultado mais condizente com o esperado matematicamente. Vejamos:
simplify( sin(x) * cos(y) + cos(x) * sin(y) )sin(x + y) == simplify( sin(x) * cos(y) + cos(x) * sin(y) )True
Perceba que usamos a função simplify. No entanto, há uma função específica para situações onde estão envolvidas funções trigonométricas, a trigsimp:
sin(x + y) == trigsimp( sin(x) * cos(y) + cos(x) * sin(y) )True
Muito embora o resultado nesse caso tenha sido o mesmo para as duas funções, a documentação recomenda o uso da trigsimp quando há funções trigonométricas envolvidas, já que o algoritmo dessa função é otimizado para essas situações.
Claro que não poderia faltar a relação trigonométrica fundamental neste artigo. Vamos usá-la para demonstrar mais uma vez que o SymPy não faz simplicações automaticamente:
sin(x)**2 + cos(x)**2Sabemos que tal soma tem resultado 1, mas o SymPy apresenta a expressão completa.
Vamos criar uma expressão e associar à uma variável expr:
expr = 2 * sin(x)**2 + 2 * cos(x)**2exprPerceba que, colocando o 2 em evidência, fica claro que tal expressão possui valor 2. Mas precisamos explicitamente solicitar a simplificação ao SymPy:
trigsimp(expr)O mesmo vale para operações sobre expressões trigonométricas:
log(expr)log(expr).trigsimp()trigsimp(log(expr))Observe acima que chamamos trigsimp como um método e diretamente, duas formas equivalentes. Particularmente acho a segunda forma mais legível, mas apenas mostrando que há as duas possibilidades.
Assim como há os procedimentos de simplificação, há os de expansão. Vamos criar uma expressão envolvendo uma das fórmulas de arco múltiplo:
expr = sin(2*x)Vimos no artigo de introdução ao SymPy que há a função expand:
expand(expr)Perceba que a expressão não foi expandida. Aqui, assim como na simplificação, há um método específico para expansão envolvendo funções trigonométricas, o expand_trig:
expand_trig(expr)Agora, sim, o resultado esperado.
Reforçando, é uma boa prática nos casos em que há funções trigonométricas envolvidas usar métodos do SymPy específicos para tais casos.
Gráficos de seno, cosseno e tangente
Não sei se o leitor é tão louco como eu, mas sou fissurado em gráficos. E os gráficos das funções trigonométricas sempre me chamaram a atenção pela natureza periódica deles. E não se pode efetivamente compreender as aplicações de tais funções sem ter uma clara noção de tal natureza.
Comecemos definindo um padrão para os gráficos do artigo. Já vimos neste artigo que o SymPy utiliza por baixo o Matplotlib para gráficos então, configurando o Matplotlib, indiretamente estamos também configurando os gráficos gerados pelas funções de plot do SymPy:
params = {
'lines.linewidth': 2.0,
'axes.labelsize': 14,
'axes.titlesize': 14,
'axes.spines.top': False,
'axes.spines.right': False,
'xtick.labelsize': 14,
'ytick.labelsize': 14,
'figure.autolayout': True,
'figure.titlesize': 20,
'figure.figsize': (10, 6),
'legend.shadow': False,
'legend.fontsize': 12,
}
plt.rcParams.update(params)Vamos primeiro fazer os gráficos das funções seno e cosseno:
plot(sympy.sin(x), sympy.cos(x), # funções
(x, -2*sympy.pi, 2*sympy.pi), # intervalo do gráfico
legend=True); # mostrar legenda com as funçõesOK, um perfil já esperado e conhecido. Mas… você provavelmente não usava x para ângulo em suas aulas de matemática. Usava letras gregas como, alfa, beta, teta… Já estamos aqui mesmo, vamos ver como usar tais letras no SymPy.
O SymPy permite passar códigos LaTeX para criar símbolos:
theta = Symbol(r'theta')
thetasin(theta), cos(theta)Ótimo! Parece ser o que queremos. Repare que o código LaTeX foi passado como uma raw string (prefixo r antes da string). Isso é para que o Python não interprete erroneamente o que faz parte do código LaTeX.
Vejamos o gráfico:
plot(sin(theta), cos(theta),
(theta, -2*sympy.pi, 2*sympy.pi),
legend=True);Infelizmente no gráfico gerado pela função plot do SymPy não aparece o símbolo, mas apenas o código LaTeX referente ao símbolo. No entanto, o Matplotlib aceita código LaTeX, a passagem de tal símbolo do SymPy para o Matplotlib que, por algum motivo, não é feita corretamente. Mas não há problemas, já vimos neste artigo que é possível extrair os dados de gráficos do SymPy e passá-los diretamente para o Matplotlib. Ou seja, eliminando a intermediação do SymPy. Para isso, seguimos o procedimento do artigo citado, associando o plot à uma variável e extraindo os dados de pontos e de labels:
p = plot(sin(theta), cos(theta),
(theta, -2*sympy.pi, 2*sympy.pi),
legend=True,
show=False)plots = []
for line in p:
data = line.get_points()
label = line.label
plots.append((data, label))Agora, vamos criar nosso próprio gráfico e passar os dados e labels obtidos:
fig, ax = plt.subplots()
for data, label in plots:
ax.plot(*data, label=f'${label}$')
ax.legend(fontsize=14)
ax.set_xlabel(r'$theta$')
ax.set_ylabel(r'$f(theta)$')
plt.show()Agora sim! Veja que os labels, que são código LaTeX, são rodeados pelo símbolo $. Tal símbolo indica para o Matplotlib que o conteúdo no interior é um código LaTeX.
Porém… se você lembrar de suas aulas de matemática, os gráficos tinham escala apresentando os ângulos radianos, usualmente em múltiplos de π. Vamos tentar, com o método MultipleLocator do Matplotlib, colocar os traços principais do eixo dos ângulos em múltiplos de π/2 e os secundários em múltiplos de π/4:
fig, ax = plt.subplots()
for data, label in plots:
ax.plot(*data, label=f'${label}$')
ax.legend()
ax.set_xlabel(r'$theta$')
ax.set_ylabel(r'$f(theta)$')
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 4))
plt.show()Isto é quase o que queremos. Não queremos a representação em float das frações, mas que elas sejam apresentadas como frações mesmos. Para isso, precisamos criar um função que faça essa formatação e usar o FuncFormatter do Matplotlib. A função a seguir, adaptada daqui e daqui, faz tal serviço.
def format_func(value, tick_number):
"""find number of multiples of pi/2"""
N = int(np.round(2 * value / np.pi))
if N == 0:
return "0"
elif N == 1:
return r"$dfrac{1}{2}pi$"
elif N == 2:
return r"$pi$"
elif N % 2 > 0:
return r"$dfrac{{{0}}}{{2}}pi$".format(N)
else:
return r"${0}pi$".format(N // 2)fig, ax = plt.subplots()
for data, label in plots:
ax.plot(*data, label=f'${label}$')
ax.legend()
ax.set_xlabel(r'$theta$')
ax.set_ylabel(r'$f(theta)$')
ax.tick_params(axis='both', which='major')
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 4))
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
plt.show()Perfeito! Caso ache necessário, pode adicionar linhas de grade para facilitar a leitura:
fig, ax = plt.subplots()
for data, label in plots:
ax.plot(*data, label=f'${label}$')
ax.legend()
ax.set_xlabel(r'$theta$')
ax.set_ylabel(r'$f(theta)$')
ax.tick_params(axis='both', which='major')
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 4))
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
ax.axhline(color="gray", zorder=-1)
ax.axvline(color="gray", zorder=-1)
ax.grid(b=True, which='major', linestyle='--', linewidth=1.5)
ax.grid(b=True, which='minor', axis='both', linestyle=':', linewidth=1)
ax.set_axisbelow(True)
plt.show()Pronto. Um gráfico fácil de ler e com escala adequada ao contexto.
Vamos agora repetir o procedimento para o gráfico de tangente. Esse é mais desafiador:
plot(tan(theta),
(theta, -2*sympy.pi, 2*sympy.pi),
legend=True);Consegue entender o que aconteceu aqui? A função da tangente apresenta uma peculiaridade. Ela não existe quando o valor de cosseno for 0 (porque a divisão por zero não está definida), portanto o domínio são todos os números reais, exceto os que zeram o cosseno.
Logo, quanto mais próximo de zero o valor do cosseno, maior o valor da tangente, de forma que a função tende ao infinito nas proximidades de tais ângulos e não está definida neles. Basicamente, estamos dizendo que há assíndotas verticais nestes ângulos.
Devido a esse comportamento de tender ao infinito, vemos valores elevados no eixo vertical. Se limitarmos o gráfico para um intervalo menor no eixo vertical, começamos a perceber o perfil que conhecemos:
plot(tan(theta), (theta, -2*sympy.pi, 2*sympy.pi), ylim=(-4, 4), legend=True);Vemos que ainda há retas que, na realidade, não deveriam estar aparecendo. Tais retas são uma tentativa do Sympy de “ligar” o extremo infinito positivo antes de uma indefinição ao extremo infinito negativo após o ângulo de indefinição. Ou seja, uma tentativa frustada, pois, na realidade, a função não é contínua.
Para resolver o problema gráfico, vamos novamente precisar extrair os dados do SymPy. Repare na célula abaixo que solicito mais pontos que o padrão com o nb_of_points visto que precisarei me livrar de alguns (as retas):
p = plot(tan(theta), (theta, -2*sympy.pi, 2*sympy.pi), ylim=(-4, 4),
legend=True, show=False, nb_of_points=1000)Vamos ver como o Matplotlib mostra o gráfico:
fig, ax = plt.subplots()
ax.plot(*p[0].get_points(), label=f'${p[0].label}$', linewidth=3)
ax.legend()
ax.set_xlabel(r'$theta$')
ax.set_ylabel(r'$tan(theta)$')
ax.tick_params(axis='both', which='major')
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 4))
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
ax.axhline(color="gray", zorder=-1)
ax.axvline(color="gray", zorder=-1)
ax.grid(b=True, which='major', linestyle='--', linewidth=1.5)
ax.grid(b=True, which='minor', axis='both', linestyle=':', linewidth=1)
ax.set_axisbelow(True)
plt.show()Como já era de se esperar, com o mesmo problema. Afinal, ainda não lidamos com ele.
Aqui usaremos o NumPy, mais especificamente o método masked_where. Tal método permite criar o que se chama de mask (máscara) no NumPy e é ideal para lidar com dados inválidos. Basicamente, vamos definir um valor a partir do qual os valores serão considerados inválidos. Na célula a seguir, considerei tal valor 20. É um valor arbitrário, poderia ser maior ou menor. Como vou limitar o gráfico entre -4 e 4, escolhi um valor um pouco maior para ter mais pontos para as curvas terem um perfil mais suavizado.
theta_values, tan_values = p[0].get_points()
tan_masked = np.ma.masked_where(np.abs(tan_values) > 20., tan_values)
fig, ax = plt.subplots()
ax.plot(theta_values, tan_masked, label=f'${p[0].label}$')
ax.legend()
ax.set_xlabel(r'$theta$')
ax.set_ylabel(r'$tan(theta)$')
ax.tick_params(axis='both', which='major')
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi / 4))
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
ax.axhline(color="gray", zorder=-1)
ax.axvline(color="gray", zorder=-1)
ax.set_ylim(-4, 4)
ax.grid(b=True, which='major', linestyle='--', linewidth=1.5)
ax.grid(b=True, which='minor', axis='both', linestyle=':', linewidth=1)
ax.set_axisbelow(True)
plt.show()Agora temos o perfil que conhecemos.
O que aprendemos? Muito Matplotlib e NumPy, espero. E, no caso do gráfico da tangente, o que costuma acontecer quando há descontinuidade numa função. Lembre-se: para “o computador” é apenas um conjunto de valores de x sendo passados para um função e gerando pares de pontos. Ele fará o possível, ou melhor, o programado, com o que foi passado, mas não compreende o conceito de descontinuidade, um conceito, uma semântica humana. Daí a necessidade de tratar os dados eliminando os valores a partir de um corte arbitrário. Quase sempre que “retas estranhas” surgem é por uma condição de descontinuidade que não foi percebida.
E outra coisa pode ser aprendida e muitas vezes é ignorada: tente reproduzir materiais que já conhece para aprender programação. Certamente que você já conhecia tais gráficos, mas pensou que teria esses detalhes para conseguir reproduzi-los fielmente?
Gráficos em 3D
Pare e pense numa palavra: hélice. O que te vem à mente? Pense no formato geométrico. Consegue relacionar com o assunto que estamos tratando?
No início da seção dos gráficos bidimensionais destaquei o perfil periódico dos gráficos. Por esse motivo, usualmente os movimentos harmônicos estudados em física de ensino médio costumam ser os primeiros exemplos aplicados das funções trigonométricas que temos contato. Ao menos formalmente, pois na vida prática temos vários, apenas não pensamos nisso.
No artigo da Wikipedia sobre a forma de hélice e relacionados, temos algumas figuras e exemplos interessantes. Por exemplo, qual a primeira coisa que aprende sobre o DNA nas aulas de biologia? A famosa dupla hélice:
Dupla hélice do DNA. Fonte: Wikipedia
Outra exemplo clássico: uma mola. Plantas como as trepadeiras com suas gavinhas. O caminho que uma partícula carregada faz em um campo magnético também é helicoidal. Só pesquisar na internet que achará mais e mais exemplos.
E tal formato pode ser obtido por equações paramétricas em coordenadas cartesianas. Por exemplo:
t = sympy.Symbol('t')
plot3d_parametric_line(cos(t),
sin(t),
t,
(t, 0, 6*sympy.pi),
);Simples, não? É um comportamento periódico, olha ali as funções seno e cosseno.
Agora olhe os seguites trechos de músicas piegas dos anos 80:
A vida vem em ondas, como um mar
Num indo e vindo infinito
Tudo vem tudo vai
Como as ondas do mar
Bom, além de aparentemente ser fonte de sofrência para músicos, ondas do mar são exemplos de comportamentos periódicos, o que até aparece figurativamente nas letras. Muito embora eu prefira lembrar do mar em grandes aventuras épicas, culpa do Iron Maiden.
Veja o seguinte gráfico, gerado pela multiplicação de duas funções trigonométricas:
plot3d(sin(y) * cos(x),
(x, -sympy.pi, sympy.pi),
(y, -sympy.pi, sympy.pi),);Consegue enxergá-lo como uma boa analogia à uma onda? Observe o comportamento de máximos e mínimos. Aqui os químicos e físicos talvez se recordem do exemplo mais clássico nessas áreas: orbitais atômicos. Sabe aqueles formatos de orbitais que fizeram você decorar no ensino médio? Olhe as equações no link, aparecem seno e cosseno nelas. Não por acaso, tais equações surgem da chamada função de onda estudada em quântica, mas isso é para detalhar em outro artigo.
Volte para a figura anterior. Imagine um plano paralelo ao plano xy e que corte o gráfico. Por exemplo, pegue um plano em z = 0.25, sendo z = f(x,y), nosso eixo vertical. O que você veria sobre esse plano? Como seria o gráfico dessa interseção, desse corte, entre a superfície e plano?
Bom, basicamente, estamos procurando o gráfico da equação sin(y) cos(x) = 0.25 concorda? Que é uma função implícita. Convenientemente, o SymPy possui o método plot_implicit para o qual podemos passar a equação e obter o gráfico:
plot_implicit(sympy.Eq(sin(y) * cos(x), 0.25),
(x, -sympy.pi, sympy.pi),
(y, -sympy.pi, sympy.pi),
);Consegue entender o gráfico? É o conjunto de pontos de interseção da superfície com o plano no valor de z = 0.25, na altura 0.25, no nível 0.25.
Imagine que, ao invés de uma onda, o gráfico represente um terreno, com vales e montanhas. Daí surge o conceito de curvas de nível, basicamente fizemos a curva de nível na altura 0.25. É um assunto importante em topografia e um exemplo clássico em aulas de cálculo em faculdades, geralmente em Cálculo 2.
O que veríamos se colocássemos várias curvas de nível em um mesmo gráfico, como se estivéssemos empilhando as curvas, mas vendo-as de cima, num mesmo plano?
Aqui precisaremos novamente de uma ajuda no NumPy e do Matplotlib, pois queremos obter diversos valores numéricos de uma equação. O SymPy possui a função lambdify que permite transformar uma expressão do SymPy em uma função que pode ser utilizada em cálculos numéricos do NumPy. E o Matplotlib possui o método contour para curvas de nível. Vejamos:
# cria função com lambdify
f = sympy.lambdify((x, y), sin(y) * cos(x), 'numpy')
# cria conjunto de valores
x_values = np.linspace(-np.pi, np.pi, 1000)
y_values = np.linspace(-np.pi, np.pi, 1000)
X, Y = np.meshgrid(x_values, y_values)
# cria curvas de nível
cp = plt.contour(X, Y, f(X, Y));
# coloca o valor de cada nível no gráfico
plt.clabel(cp);O que esquema de cores é o mesmo utilizado no gráfico em 3D. Compare as curvas de nível com a superfície 3D para ter certeza que compreendeu o que foi feito.
Podemos definir o número de níveis que queremos no gráfico:
cp = plt.contour(X, Y, f(X, Y), 20);
plt.clabel(cp);É muito comum, quando queremos mostrar muitos níveis, utilizar mapas colorizados e apresentar uma escala de cores. Para isso, temos o método contourf (o f é de fill, “preenchido” em inglês):
plt.contourf(X, Y, f(X, Y), 30);
plt.colorbar();Gráfico bem bonito e alucinógeno. O nosso padrão periódico é claramente percebido aqui, mesmo que tenhamos “perdido” uma das dimensões do gráfico.
Tá vivo ainda? Esperava ver isso tudo num artigo de funções trigonométricas? Tem mais um pouco, mas tá acabando…
Funções hiperbólicas
Se as funções trigonométricas ordinárias já assustam algumas pessoas, as hiperbólicas então… Mas, se você chegou até aqui, é porque consegui mostrar o quão interessantes, e úteis, são as funções trigonométricas. E igualmente são as hiperbólicas, como pretendo mostrar.
A origem geométrica pode ser vista aqui, mas neste artigo pretendo ir mais direto ao ponto das aplicações. Assim, vejamos brevemente as definições.
As funções hiperbólicas podem ser definidas a partir de funções exponenciais:
(exp(x) + exp(-x))/2simplify( (exp(x) + exp(-x))/2 )(exp(x) - exp(-x))/2simplify( (exp(x) - exp(-x))/2 )simplify(sinh(x) / cosh(x))Mas qual a relação existente entre as funções hiperbólicas e as trigonométricas? Por que estão aparecendo no mesmo artigo? Porque as funções trigonométricas também podem ser definidas a partir de funções exponenciais, mas só que são funções exponenciais complexas de acordo com a fórmula de Euler:
eix = cos(x) + i sin(x)
Que podemos representar em um plano complexo:
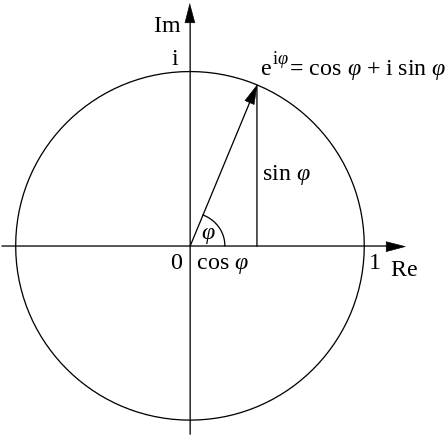
O SymPy possui o símbolo I para indicar complexo:
exp(sympy.I * x)Podemos usar o método rewrite para solicitar que o SymPy reescreva uma dada expressão utilizando outras funções matemáticas:
exp(sympy.I * x).rewrite(cos)Assim, vemos acima que surge a igualdade da fórmula de Euler.
Podemos solicitar que o SymPy reescreva as funções seno e cosseno em forma exponencial:
sin(x).rewrite(exp)cos(x).rewrite(exp)Veja que são muito similares às definições de seno e cosseno hiperbólicos, sendo a diferença a presença de argumentos complexos nas exponenciais.
Ora, isso significa que se passarmos argumentos complexos para as funções seno e cosseno, vão surgir as funções seno e cosseno hiperbólicas:
sin(sympy.I * x).rewrite(exp)expand_trig(sin(sympy.I * x))cos(sympy.I * x).rewrite(exp)expand_trig(cos(sympy.I * x))Vemos, portanto, que as funções trigonométricas e hiperbólicas estão intimamente relacionadas. Em breve farei artigos sobre números complexos então, se teve dificuldade em entender o que foi discutido aqui, em breve retomarei o assunto. Enquanto isso, esse link mostra em mais detalhes as relações entre trigonométricas e hiperbólicas e pode ajudar.
Assim como as funções trigonométricas, também há identidades importantes dentre as funções hiperbólicas como, por exemplo:
cosh(x)**2 - sinh(x)**2simplify(_)Vejamos o gráfico do seno, do cosseno e da tangente hiperbólicos:
plot(sinh(x), cosh(x), tanh(x),
(x, -3, 3),
ylim=(-3, 3),
legend=True,);Aqui começa a ficar (mais) interessante.
Gráficos de catenária e de catenoide
Observe as duas fotos a seguir:


Exemplos de catenárias. Fonte: Wikipedia
Consegue relacionar as fotos com alguma das curvas apresentadas no gráfico anterior?
As duas fotos ilustram exemplos reais de catenárias. Catenária é a curva assumida por uma corrente, ou cabo flexível, suspensa fixada apenas por suas extremidades e sujeita somente à força de seu próprio peso (gravidade). São importantes em engenharia e arquitetura. Uma força aplicada em um ponto qualquer da curva é distribuída igualmente por todo material, proporcionando maior estabilidade à estrutura. É amplamente utilizada na construção de arcos arquitetônicos, domos de catedrais e iglus. Há diversos exemplos neste link.
A definição matemática de uma catenária em coordenadas cartesianas é bem simples:
a = Symbol('a')
catenary = a * cosh(x/a)
catenaryOnde a é uma constante. Vejamos o efeito dessa constante criando gráficos para alguns valores:
plots = []
for i in range(1, 6):
expr = catenary.subs({a: i})
p = plot(expr, (x, -6, 6), show=False)
data = p[0].get_points()
plots.append(data)
fig, ax = plt.subplots()
for i, p in enumerate(plots, 1):
ax.plot(*p, label=f'a = {i}', linewidth=3)
ax.set_ylim(0, 10)
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title(r"Catenary: $y = a cosh left( dfrac{x}{a} right)$")
plt.show()Graficamente, vemos que o a define a “abertura” da curva. Mas, estruturalmente, considerando como exemplo uma corrente, tal fator está relacionado com a tensão horizontal na corrente e com o peso da mesma. Faz sentido, concorda?
Agora, olhe a seguinte foto:

Exemplo de um catenoide. Fonte: Wikipedia
Sim, é uma bolha de sabão que foi esticada pelos anéis azuis na foto. Olhe o formato da superfície gerada e se prepare para um exercício mental. Volte no gráfico anterior, escolha a catenária de maior abertura, ou seja, com a = 5. Mentalmente, deite-a de lado, apontando sua abertura para a esquerda, e rode-a ao redor de um eixo vertical imaginário. Parabéns, acabou de gerar um catenoide em sua mente, que é muito similar ao fenômeno ilustrado na foto.
Um catenoide é uma superfície mínima, ou seja, uma superfície em que fixados todos os pontos do bordo, quaisquer dois pontos são ligados por infinitas curvas, sendo que uma delas é uma catenária. Tornando um pouco mais fácil de entender, é uma superfície com a menor área possível dada suas bordas (condições de contorno). Sua curvatura média é zero em todos os pontos.
É uma estrutura muito estudada, desde estudos de estruturas moleculares auto-organizadas, passando pelo estudo de estrutura tênsil em arquitetura, até a avaliação de tensão superficial de materiais.
Sua definição em um plano cartesiano pode ser feita pelas seguintes equações paramétricas:
c, v = sympy.symbols('c v')
catenoid_x = c * cosh(v / c) * cos(t)
catenoid_y = c * cosh(v / c) * sin(t)
catenoid_z = v
catenoid_x, catenoid_y, catenoid_zVeja que há funções trigonométricas e hiperbólicas nas definições. Temos uma constante c real não nula, uma variável t real no intervalo de [-π, π) e uma variável v real.
Vamos substituir a constante c por algum valor, por exemplo, 1, e gerar nossa superfície:
catenoid_x = catenoid_x.subs({c: 1})
catenoid_y = catenoid_y.subs({c: 1})
catenoid_x, catenoid_y, catenoid_zplot3d_parametric_surface(catenoid_x, catenoid_y, catenoid_z,
(t, -sympy.pi, sympy.pi),
(v, -1, 1),);Muito parecido com a foto, certo?
E qual o efeito dessa constante? Vamos substituir por 0.5:
catenoid_x = c * cosh(v / c) * cos(t)
catenoid_y = c * cosh(v / c) * sin(t)
catenoid_x = catenoid_x.subs({c: 0.5})
catenoid_y = catenoid_y.subs({c: 0.5})
plot3d_parametric_surface(catenoid_x, catenoid_y, catenoid_z,
(t, -sympy.pi, sympy.pi),
(v, -1, 1),);Vemos que “afinou a cintura” do catenoide.
Conclusão e mais artigos sobre SymPy
Foi uma longa viagem por funções trigonométricas e hiperbólicas, mas espero ter tornado o assunto interessante. Infelizmente o ambiente de ensino por vezes foca muito na matemática e esquece de mostrar os exemplos reais, aplicações e conexões entre assuntos. Se, além de você ter achado interessante, ainda deu para aprender um pouco de Python, meu objetivo foi alcançado.
Caso queira saber quando novos artigos são disponibilizados, siga o Ciência Programada nas redes sociais. A lista completa de artigos sobre SymPy pode ser vista na tag SymPy.
Até a próxima.