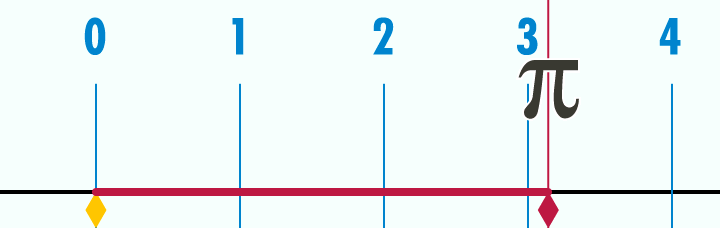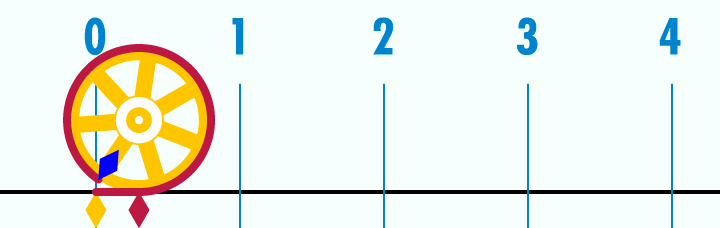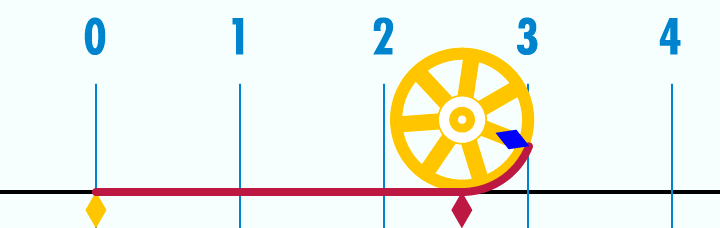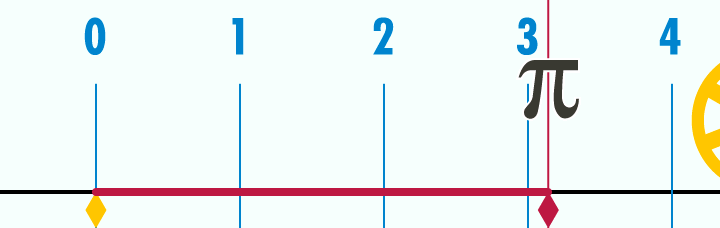
O número π é uma constante matemática que é a razão entre a circunferência de um círculo e seu diâmetro. É um número irracional, ou seja, que não pode ser expresso exatamente como a razão entre dois números inteiros.
Ser um número irracional tem como consequência uma representação decimal infinita e sem repetições. Assim, durante milênios matemáticos buscam melhorar seu entendimento sobre o número π, e obter seu valor com maior acurácia.
Neste artigo, vamos passar pela história do número π e aprender um pouco de programação Python no caminho.
Tópicos
Definição
Na introdução deste artigo demos uma definição por extenso de π e mostramos uma animação que ajuda a entender visualmente tal definição. Agora, vamos para uma definição matemática. Existem diversas formas de definir π matematicamente. Aqui, adotaremos uma definição baseada em cálculo.
A circunferência de um círculo é o comprimento do arco sobre o perímetro de tal círculo. Considerando, por exemplo, o círculo unitário dados em coordenadas cartesianas, podemos obter π como resultado de uma integral:
Aqui no Ciência Programa temos uma categoria apenas para artigos que utilizam SymPy. Vejamos como este pacote Python lida com esta integral:
# configuração para outputs melhores no artigo, pode ser ignorado
from sympy import init_printing
init_printing(use_latex='png', scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
from sympy import integrate, Symbol, sqrt, Integral
x = Symbol('x')
expr = 1 / sqrt(1 - x**2)
Integral(expr, (x, -1, 1))Acima, temos a representação da integral. Para resolvê-la, podemos usar o método doit do objeto Integral ou utilizar diretamente a função integrate:
Integral(expr, (x, -1, 1)).doit()integrate(expr, (x, -1, 1))Veja que o resultado da integral realmente é π.
Agora, o cálculo como conhecemos hoje teve seu desenvolvimento iniciado apenas no século XVII. Antes, como π era definido? Quais aproximações eram utilizadas?
Aproximações de π
Ao longo da história, diversas aproximações do valor de π já foram utilizadas. Uma lista em ordem cronológica de aproximações de π pode ser encontrada neste link.
História antiga
A aproximação mais simples de todas é aproximar o valor de π para 3. Os matemáticos babilônicos adotavam esta aproximação quando pertinente (sabiam que era uma aproximação). E que atire a primeira pedra o engenheiro que nunca utilizou esta aproximação 🙂
Na história antiga, temos diversas aproximações utilizadas por babilônicos, egípcios, gregos, indianos… apenas para listar algumas: 25/8, 256/81, 339/108. Todas estas frações aproximam π com erros menores que 1 %.
Cerca de 250 AC, o matemático grego Arquimedes, usando o método da exaustão, demonstrou que o valor de π deveria ser maior que 223/71 e menor que 22/7. Neste método, polígonos são inscritos e circunscritos em circunferências, aumentando sucessivamente a quantidade de lados buscando se aproximar cada vez mais à forma de circunferência.
Para mais detalhes do trabalho de Arquimedes, recomendo o livro Arquimedes: uma porta para a ciência de Jeanne Bendick, da incrível Coleção Imortais da Ciência. Clique nos links ou na imagem a seguir para mais detalhes.
Cerca de um século depois, Ptolomeu usou o valor de 377/120, a primeira aproximação conhecida com 3 casas decimais corretas.
Ao longo dos séculos, o método geométrico de Arquimedes foi sendo melhorado e, no século XVII, tais melhorias já haviam aproximado o valor de π até dezenas de casas decimais corretas.
Mas o que mudou ao se chegar no século XVII? Séries infinitas.
A revolução das séries infinitas
Já temos um artigo sobre séries infinitas no Ciência Programada. Aqui utilizaremos um pouco do visto no artigo citado, não deixe de ler o link depois 😉
Uma série infinita é a soma de termos de uma sequência infinita. Com equações baseadas em séries infinitas, um grande avanço na obtenção de valores mais precisos para π foi realizado. Diversas equações foram obtidas, por diversos matemáticos orientais e ocidentais. Algumas equações podem ser vistas aqui. Neste artigo, selecionaremos duas apenas para ilustrar o poder das séries infinitas.
As séries escolhidas são apresentadas a seguir. A escolha delas para esse artigo se deve pelo aspecto didático. São expressões relativamente simples e de matemáticos muito relevantes, Gottfried Leibniz e Leonhard Euler. Nos links de cada matemático, coloquei artigos que falam um pouco sobre a história de cada série para aqueles que se interessarem, vale a leitura.
No início do artigo, mostrei como um pacote para matemática simbólica como o SymPy pode ser utilizado para representar estes somatórios. Meu objetivo agora é outro: mostrar como estas fórmulas tendem a se aproximar do valor de π quanto mais termos forem utilizados. Vou utilizar Python bem básico aqui, com a biblioteca matemática padrão e Matplotlib para gráficos.
As duas séries podem ser escritas facilmente na forma de funções, como mostra a célula a seguir. Veja que os corpos de ambas as funções são similares. Uma variável, result, é iniciada com o valor zero e tal valor é incrementado em loops que dependem do número de termos desejado. O retorno é o valor final dessa variável após o loop e operações matemáticas apresentadas nas expressões das séries.
import math
def pi_leibniz(number_of_terms):
result = 0
for k in range(number_of_terms):
result += 1/((4 * k + 1) * (4 * k + 3))
return 8 * result
def pi_euler(number_of_terms):
result = 0
for k in range(1, number_of_terms + 1):
result += 1/k**2
return math.sqrt(6 * result)Com estas funções, podemos mostrar graficamente que as séries tendem para o valor de π com o aumento de termos utilizados nos somatórios:
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset
plt.style.use('ggplot')
n = range(1, 101)
fig, ax = plt.subplots(figsize=(10, 6))
axins = zoomed_inset_axes(ax, 3, loc='center')
for axis in (ax, axins):
axis.hlines(math.pi, xmin=min(n), xmax=max(n),
label='Valor de pi',
linestyle='--', color='red')
axis.plot(n, [pi_leibniz(i) for i in n],
label='Leibniz',
color='green')
axis.plot(n, [pi_euler(i) for i in n],
label='Euler',
color='blue')
x1, y1 = 80, 3.12
x2, y2 = 100, 3.15
axins.set_xlim(x1, x2)
axins.set_ylim(y1, y2)
axins.set_facecolor('whitesmoke')
mark_inset(ax, axins, loc1=2, loc2=4, fc="none", ec="0.6")
ax.legend()
ax.set_ylabel('Valor aproximado')
ax.set_xlabel('Número de termos')
ax.set_title('Aproximação de $\pi$ por séries')
plt.show()Observe na região em destaque ampliado do gráfico como as duas séries se aproximam do valor de referência cada vez mais.
Seria interessante saber o erro percentual de cada aproximação. Podemos criar uma função para calcular o erro de um valor dado um valor de referência e construir um gráfico para a variação de erro de cada série:
def error(calculated, expected):
return (calculated - expected) / expected
from matplotlib.ticker import PercentFormatter, MultipleLocator
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(n[9:], [error(pi_leibniz(i), math.pi) for i in n[9:]],
label='Leibniz', color='green')
ax.plot(n[9:], [error(pi_euler(i), math.pi) for i in n[9:]],
label='Euler', color='blue')
ax.legend()
ax.set_ylabel('Erro / %')
ax.set_xlabel('Número de termos')
ax.yaxis.set_major_formatter(PercentFormatter(1, symbol=None))
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.set_title('Aproximação de $\pi$ por séries - Erro percentual')
plt.show()Veja como a série de Leibniz rapidamente fornece aproximações com menos de 1 % de erro. A de Euler necessita de 30 termos para entrar nessa faixa de erro.
Teoricamente, poderíamos continuar adicionando termos para obter um erro cada vez menor:
terms = (100, 500, 1000, 5000)
print('Erro percentual x termos')
print('Termos Leibniz Euler')
for number in terms:
error_leibniz = error(pi_leibniz(number), math.pi) * 100
error_euler = error(pi_euler(number), math.pi) * 100
print(f'{number:4} {error_leibniz:.1E} {error_euler:.1E}')Erro percentual x termos Termos Leibniz Euler 100 -1.6E-01 -3.0E-01 500 -3.2E-02 -6.1E-02 1000 -1.6E-02 -3.0E-02 5000 -3.2E-03 -6.1E-03
Mas qual o limite? Até onde aproximar? Aliás, para que obter valores com cada vez mais casas decimais para π?
Para que saber mais casas decimais do valor de π?
Em um artigo sobre nossa atmosfera, escrevi sobre a importância de não fazer arredondamentos em constantes matemáticas envolvidas em nossas contas. Ou, pelo menos, evitar arredondamentos drásticos, usando menos algarismos significativos que os envolvidos em nossos dados experimentais. Essa é uma má prática que é propagada em disciplinas de exatas, mesmo em universidades. Há padrões bem estabelecidos de arredondamento e de propagação de incertezas. Use-os.
Mas e quando se trata de um valor como o de π, que é irracional? Até onde compensa o esforço de se obter cada vez mais casas decimais?
No vídeo a seguir (clique na imagem para assistir o vídeo), o matemático James Grime explica que 39 casas decimais para π são suficientes para calcular a circunferência do universo observável com precisão de um átomo de hidrogênio.
Em um recente artigo da NASA, um dos engenheiros do Laboratório de Propulsão da organização explica que são utilizadas 15 casas decimais na instituição. Clique no link para detalhes, mas basicamente o engenheiro explica ser o suficiente para a precisão necessária em viagens interestelares.
No momento que escrevo este artigo, o recorde de números de casas decimais para π é da ordem de trilhões! E existem motivos para a busca contínua por mais algarismos:
- é uma forma de testar supercomputadores
- avaliar algoritmos matemáticos
- testar algoritmos de números aleatórios
E, talvez, o principal motivo por trás da busca é a inerente vontade humana de quebrar recordes 🙂
Como são obtidos valores com tantas casas decimais?
Séries que convergem rapidamente
Os grandes avanços tecnológicos e nos estudos matemáticos nos possibilita hoje ter formas mais rápidas de se ter valores para π com a precisão desejada. As séries apresentadas anteriormente tinham o problema de necessitarem muitos termos para atingirem margens de erros aceitáveis. Então, há um custo de processamento e de memória.
No início do século XX, o matemático indiano Srinivasa Ramanujan desenvolveu uma fórmula de rápida convergência. Tal fórmula foi referência para, algumas décadas depois, os irmãos Chudnovsky desenvolverem outra série que produz 14 dígitos de π por termo. Seguem as fórmulas:
A matemática por trás de cada fórmula vai um pouco além do objetivo deste artigo, mas os interessados podem clicar nos links que coloquei acima. A fórmula de Ramanujan possibilitou chegar a recordes de milhões de dígitos na década de 80 e os recordes atuais de trilhões de dígitos utilizaram a fórmula de Chudnovsky.
Podemos criar funções em Python para reproduzir tais fórmulas, conforme a célula a seguir. Repare que a construção das funções é bem similar ao visto para as séries de Leibniz e Euler:
def pi_ramanujan(number_of_terms):
result = 0
for k in range(number_of_terms):
result += (math.factorial(4 * k) * (1103 + 26390 * k)) / (math.factorial(k)**4 * 396**(4*k))
return 1 / ((2 * math.sqrt(2) / 9801) * result)
def pi_chudnovsky(number_of_terms):
result = 0
for k in range(number_of_terms):
result += (math.factorial(6 * k) * (13591409 + 545140134 * k)) / (math.factorial(3*k) * math.factorial(k)**3 * (-640320)**(3*k))
return 1 / ((12 / 640320**(3/2)) * result)Agora, podemos refazer o gráfico de comparação entre as séries, acrescentando as duas novas:
fig, ax = plt.subplots(figsize=(10, 6))
axins = zoomed_inset_axes(ax, 3, loc='center')
for axis in (ax, axins):
axis.hlines(math.pi, xmin=min(n), xmax=max(n),
label='Valor de pi',
linestyle='--', color='red')
axis.plot(n, [pi_leibniz(i) for i in n],
label='Leibniz',
color='green')
axis.plot(n, [pi_euler(i) for i in n],
label='Euler',
color='blue')
axis.plot(n, [pi_ramanujan(i) for i in n],
label='Ramanujan',
color='orange')
axis.plot(n, [pi_chudnovsky(i) for i in n],
label='Chudnovsky',
color='purple')
x1, y1 = 80, 3.12
x2, y2 = 100, 3.15
axins.set_xlim(x1, x2)
axins.set_ylim(y1, y2)
axins.set_facecolor('whitesmoke')
mark_inset(ax, axins, loc1=2, loc2=4, fc="none", ec="0.6")
ax.legend()
ax.set_ylabel('Valor aproximado')
ax.set_xlabel('Número de termos')
ax.set_title('Aproximação de $\pi$ por séries')
plt.show()Veja que nem dá para diferenciar as duas novas séries entre si na escala do gráfico, mesmo na região ampliada. E já há dígitos corretos desde o início de ambas as séries, havendo sobreposição com a linha de referência.
E como sabemos que os dígitos estão corretos?
Foram desenvolvidos métodos de extração de dígitos, que podem ser utilizados para verificar qual o dígito em uma determinada posição. Futuramente devo escrever a respeito de tais métodos, mas já fica o link para os interessados.
Recomendações de leitura
Para mais detalhes do trabalho de Arquimedes, recomendo o livro Arquimedes: uma porta para a ciência de Jeanne Bendick, da incrível Coleção Imortais da Ciência. Clique nos links ou na imagem a seguir para mais detalhes.
Para matemática em geral, há O livro da matemática, da coleção As grandes ideias de todos os tempos. Clique nos links ou na imagem a seguir para mais detalhes.
Por fim, um bom livro para iniciantes em Python é o Automatize tarefas maçantes com Python. Um livro com exemplos práticos e de fácil leitura. Clique nos links ou na imagem a seguir para mais detalhes.
Conclusão
Neste artigo vimos como podemos criar funções em Python para realizar somatórios. Mais que isso, no contexto histórico de estudos de um dos números mais famosos da matemática, o π. Com o uso de Python, vemos claramente como os algoritmos atuais são mais eficientes que os desenvolvidos há alguns séculos. E, ainda, como tal evolução pode ser melhor compreendida graficamente.
Acompanhe o projeto Ciência Programada nas redes sociais para saber quando são publicados novos artigos, em breve escreverei mais sobre o número π 😉
Até a próxima.