O início dos cursos de cálculo costuma ser abstrato pelo conceito de limite, que vimos em um artigo recente. Mas, logo passa a ser mais palpável com a introdução do conceito de derivada, que possui diversas aplicações práticas evidentes.
Neste artigo, veremos como trabalhar com derivadas com o SymPy, pacote da linguagem Python.
Tópicos
Conceito de derivada e sua interpretação
Vamos lembrar um pouco de cálculo para facilitar a leitura do artigo. Observe a animação abaixo. Nela temos uma curva de uma função qualquer, a marcação de dois pontos, A e B, e a visualização do triângulo formado para obter a variação da quantidade do eixo y e a do eixo x com auxílio de um terceiro ponto C. Na animação, os pontos vão se aproximando cada vez mais. Observe que, no limite em que os pontos se tornam mais próximos, a hipotenusa do triângulo, inicialmente uma reta secante da curva, torna-se uma reta tangente no ponto de virtual encontro A. A reta azul é a tangente no ponto A, apresentada justamente para mostrar como a secante se aproxima cada vez mais de uma tangente.
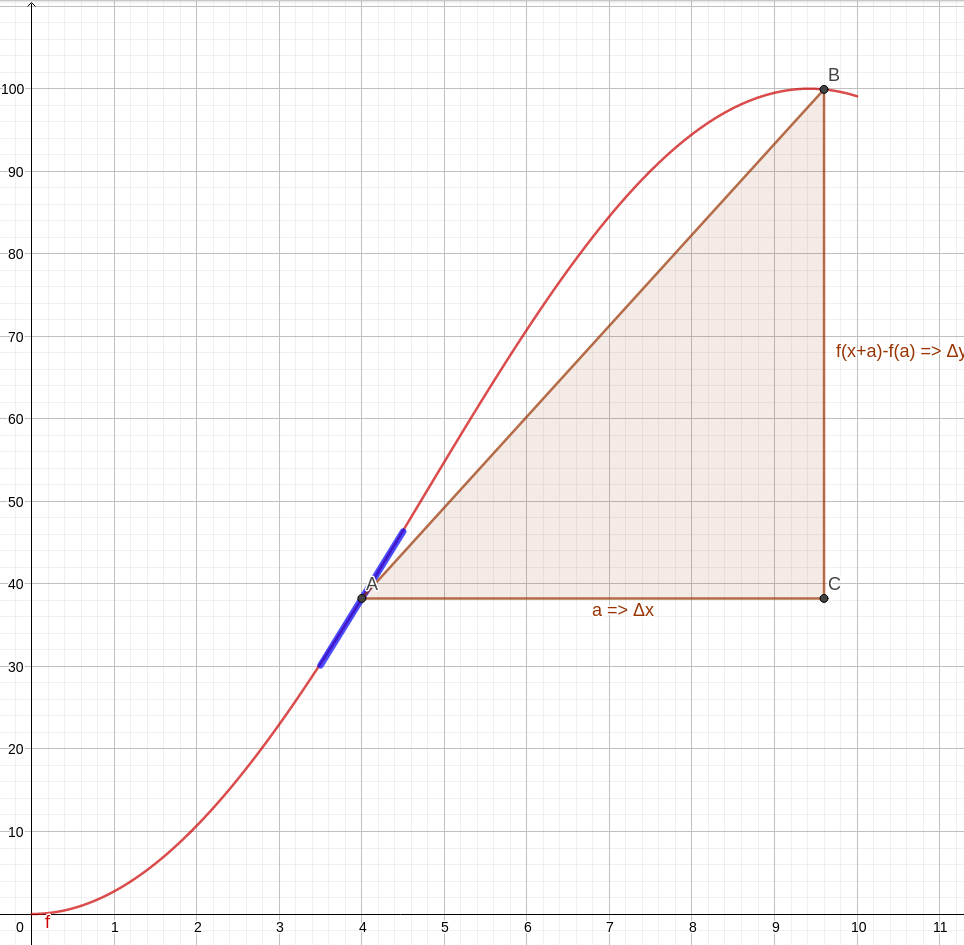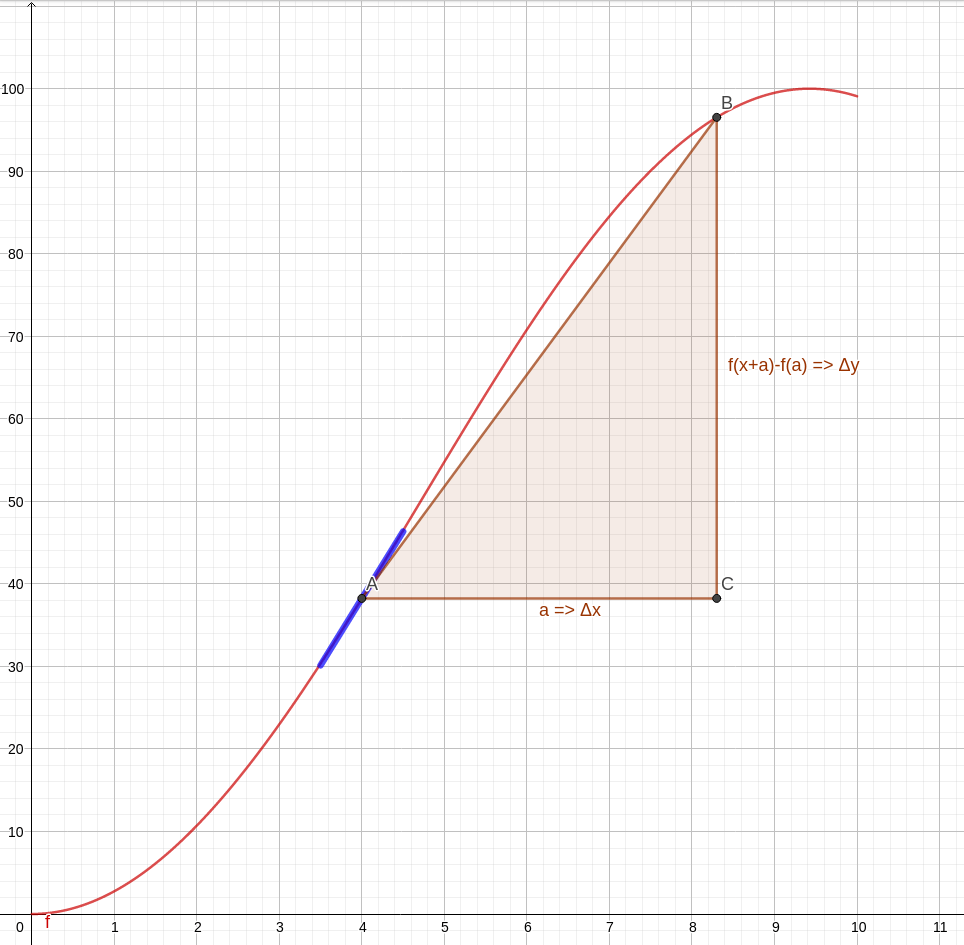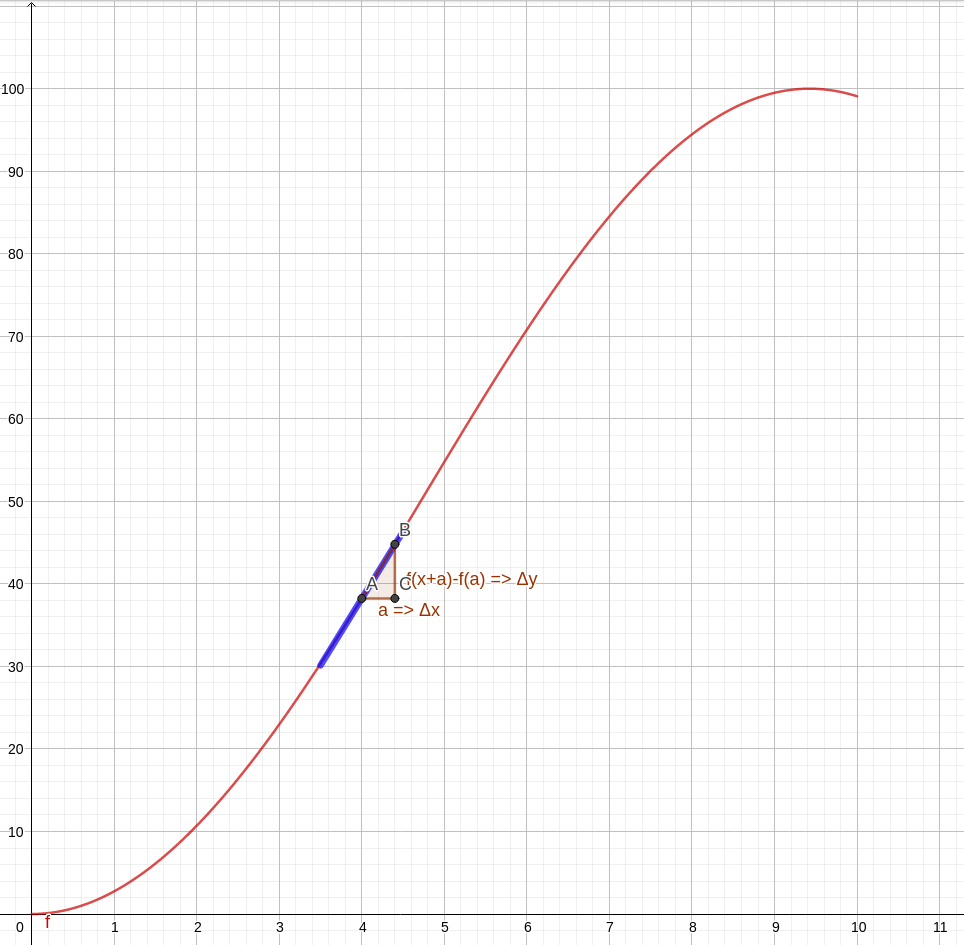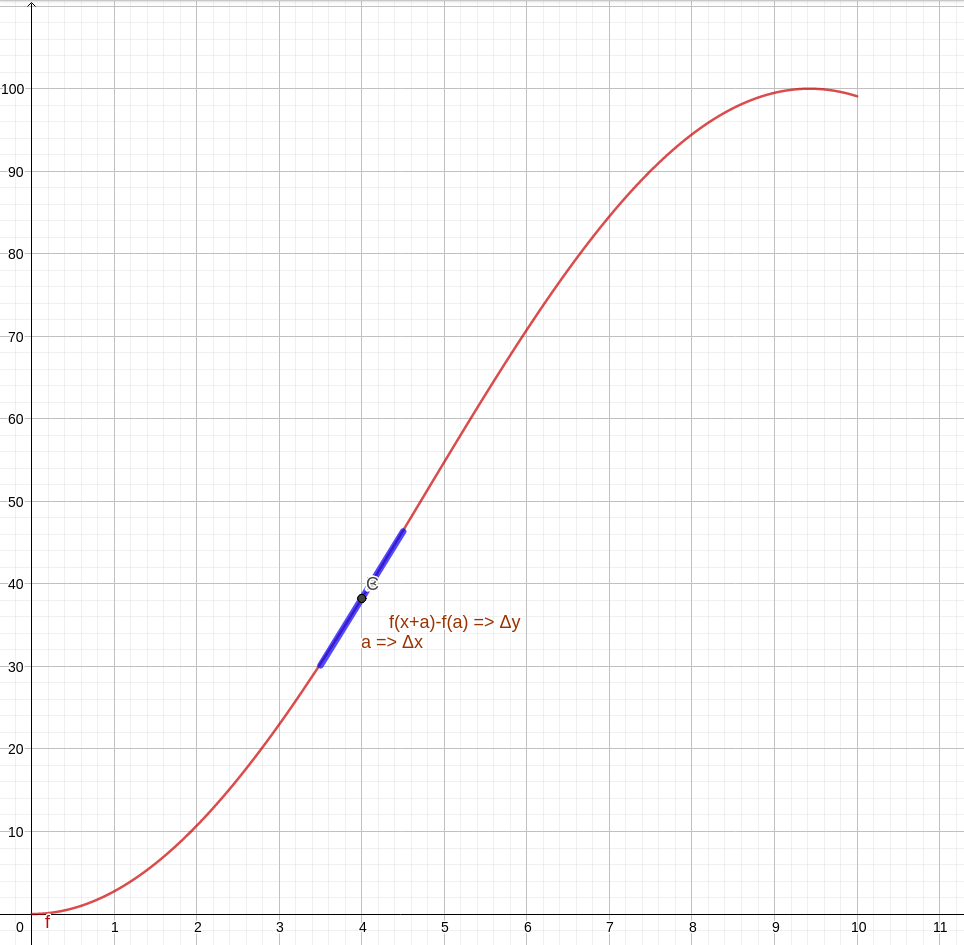
Veja que no texto aparece a palavra limite, e já escrevemos sobre o conceito de limite. Basicamente, visualizamos na animação que a reta secante se aproxima de uma tangente no limite onde os pontos A e B se aproximam. Podemos formalizar melhor escrevendo que a inclinação da reta tangente a (a, f(a)) deve ser
\lim\limits_{h \to 0} \frac{f(a + h) - f(a)}{h}Dizemos que uma função f é diferenciável em a se o limite acima existe. Neste caso, o limite é representado por f'(a) e chamado de derivada de f em a. Voltaremos à essa ideia de reta tangente e suas consequências mais adiante no artigo.
Mas, e daí? E daí que essa ideia de uma reta tangente à uma curva leva a diversas aplicações. É a origem da ideia de velocidade instantânea em física, por exemplo. Afinal, podemos visualizar instantaneidade como sendo duas medições em um intervalo de tempo muito curto, virtualmente no limite deste intervalo tendendo a zero. Assim como os pontos em nossa animação. Inclusive, já escrevemos como podemos utilizar Python para determinar a velocidade do Usain Bolt, atleta campeão olímpico e mundial, e no artigo utilizamos exatamente esta ideia e um pouco de cálculo 🙂
Neste artigo focaremos mais na parte operacional, mostrando como lidar com funções e suas derivadas com SymPy. Mas é sempre importante ter em mente a interpretação e aplicações do que estamos fazendo.
A função diff
Para iniciar, vamos considerar uma função bem simples:
f(x) = x^3Das simples regras de derivação que são estudadas em disciplinas introdutórias de cálculo, sabemos que:
f'(x) = 3x^2 \qquad f''(x) = 6x \qquad f'''(x) = 6Mas, como obtemos tais resultados com o SymPy? Precisamos utilizar a função diff do pacote. Vejamos, começando por importar o necessário:
# configuração para outputs melhores no artigo, pode ser ignorado
from sympy import init_printing
init_printing(use_latex='png', scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
from sympy import diff, SymbolVamos criar o símbolo necessário para representar x e criar nossa variável que representará a função. Em seguida, vamos solicitar a primeira derivada, passando a função e a variável segundo a qual a função será derivada:
x = Symbol('x')
f = x**3
diff(f, x)Simples, não? E para derivadas de ordem superior, basta passar como terceiro parâmetro a ordem. Por exemplo, para a derivada segunda:
diff(f, x, 2)E para a derivada terceira:
diff(f, x, 3)Para casos de funções mais complicadas, aprendemos em cálculo diversas regras de derivação como as regras de produto, divisão, da cadeia, dentre outras. O SymPy lida de forma fluida com tais casos, fornecendo diretamente o resultado final. Veja os exemplos a seguir, compare os resultados com os obtidos manualmente aplicando regras de derivação, aproveitando para estudar cálculo 😉
from sympy import sin, cos, exp
# regra do produto
diff(x**2 * sin(x), x)# regra da cadeia
diff(sin(x**2))# regra do quociente
diff(x**2 / sin(x), x)Observe que no resultado acima podemos escrever como uma única divisão, deixando mais explícita a regra do quociente. Para isso, usamos o método factor já abordado em outro artigo da série sobre o SymPy:
diff(x**2 / sin(x), x).factor()Equações diferenciais
Equações diferenciais possuem diversas aplicações, constituindo um mundo à parte dentro de cálculo. Certamente aparecerão com frequência aqui no site. Já vimos em outro artigo como usar a função solve para resolver as equações comuns que são estudadas no ensino médio. Agora, vejamos a função dsolve para equações diferenciais.
Já vimos neste e em outros artigos que podemos definir símbolos no SymPy com a classe Symbol ou com a função symbols, para representar variáveis e constantes em nossas expressões e equações. Para deixar explícito quando se trata de uma função, podemos usar a classe Function. Vamos importar o necessário e mostrar a criação de uma representação de uma função f:
from sympy import Function, dsolve, Eq
f = Function('f')
f(x)Agora que temos nossa função, vamos criar a equação diferencial
f(x) - f'(x) = 0Para isso, vamos utilizar a classe Eq e a função diff:
eq_dif = Eq(f(x) - diff(f(x), x), 0)
eq_difVeja acima que usamos nossa função f escrevendo f(x), para indicar a variável da função. Uma notação igual à mais utilizada em cálculo. Agora, basta passar tal equação para a função dsolve indicando que é para ser resolvida em função de f(x):
dsolve(eq_dif, f(x))Concorda com o resultado? Lembre-se, a função exponencial tem a curiosidade de ser igual à sua derivada 😉 Isso vale também para múltiplos desta função, daí a indicação de que pode haver uma constante C_1 multiplicando a função. Exatamente a mesma notação que costuma ser utilizada em aulas de cálculo.
Retas tangentes
Por definição, a reta tangente à uma função f(x) em x = x_0 é a reta que passa pelo ponto (x_0, f(x_0)) e tem a mesma inclinação que a função neste ponto. Tal reta é descrita pela equação
T(x) = f(x_0) + f'(x_0) (x - x_0)Vejamos este conceito partindo da função bem simples a seguir:
f(x) = \frac{1}{2} x^2Comecemos criando a função com o SymPy:
from sympy import S
f = S('1/2')*x**2
fAgora, criemos a representação de sua derivada:
df = diff(f, x)
dfDe acordo com a definição, podemos criar um representação para a reta T:
x0 = Symbol('x_0')
T = f.subs({x: x0}) + df.subs({x: x0}) * (x - x0)
TAssim, se quisermos obter a reta tangente à nossa função f em x_0 = 1 basta:
T.subs({x0: 1})Pela definição, tal reta possui o mesmo valor e a mesma inclinação que a função f(x) em x = 1. Vejamos:
# verificando que T(x0) == f(x0)
T.subs({x0: 1}).subs({x: 1}) == f.subs({x: 1})True
# verificando que a inclinação de T é a mesma da função no ponto desejado
diff(T, x).subs({x0: 1}) == diff(f, x).subs({x: 1})True
Fica mais fácil de visualizar com um gráfico. Observe no gráfico gerado pelo código abaixo a função e a reta tangente à mesma em x_0 = 1:
from sympy.plotting import plot
import matplotlib.pyplot as plt
def move_sympy_plot_to_axes(sympy_plot, plt_ax):
"""Moves a SymPy plot to a Matplotlib axes
Adapted from: https://stackoverflow.com/a/46813804/8706250
Parameters
----------
sympy_plot : SymPy plot
plt_ax : Matplotlib axes
"""
backend = sympy_plot.backend(sympy_plot)
backend.ax = plt_ax
backend._process_series(backend.parent._series, plt_ax, backend.parent)
backend.ax.spines['right'].set_color('none')
backend.ax.spines['bottom'].set_position('zero')
backend.ax.spines['top'].set_color('none')
plt.close(backend.fig)
fig, ax = plt.subplots(figsize=(8, 6))
p1 = plot(f, (x, -3, 3), show=False, label=r'$f(x) = \frac{1}{2}x^2$')
p2 = plot(x-S('1/2'), (x, -3, 3), show=False, label=r"$f'(x) = x - \frac{1}{2}$")
move_sympy_plot_to_axes(p1, ax)
move_sympy_plot_to_axes(p2, ax)
ax.scatter(1, 1/2, color='red', label='Ponto (1, 1/2)')
ax.set_title('Derivada como inclinação da reta tangente em um ponto \n')
ax.legend()
plt.show()Conclusão
Matou a saudade das aulas de cálculo? Vimos como é simples trabalhar com derivadas em SymPy e usaremos esta simplicidade em muitos dos artigos futuros aqui do site.
Acompanhe o projeto Ciência Programada nas redes sociais para saber quando são publicados novos artigos, em breve escreverei mais sobre cálculo 🙂
A lista completa de artigos sobre SymPy pode ser vista na categoria SymPy aqui do site.
Até a próxima.




