Já escrevemos aqui no site sobre os conceitos de limite e derivada e como podemos fazer contas relacionadas com Python. Seguindo na nossa jornada de cálculo, neste artigo veremos como trabalhar com integrais com o SymPy e o SciPy, pacotes da linguagem Python. No caminho, teremos algumas noções de métodos numéricos.
Há duas abordagens ao cálculo integral. Uma considera a integral como uma antiderivada. Isto é, a integração é considerada o inverso da diferenciação. A outra considera a integral como sendo a soma de muitos elementos infinitesimais. Esta segunda abordagem é a que permite atribuir significado físico a uma integral. Vejamos um pouco de cada uma.
Tópicos
Integral como uma antiderivada
Em cursos de cálculo, usualmente representamos a diferenciação de uma função y = f(x) como:
\frac{dy}{dx} = \frac{df(x)}{dx} = f'(x)Que também podemos representar na forma diferencial
dy = f'(x)dxInclusive, já vimos como lidar com derivadas no SymPy neste artigo.
No nosso contexto, podemos nos fazer a seguinte pergunta: qual função F(x), quando derivada, resulta na função f'(x)? Tal função é a chamada integral da diferencial e simbolizada como
F(x) = \int f'(x) dxExemplo, sendo f'(x) = 2x, a função que buscamos é
F(x) = \int 2xdx = x^2 + CRepare na constante de integração C. Que atire a primeira derivada quem nunca esqueceu de escrever a constante de integração numa prova de cálculo! Tendo em vista as regras de derivação estudadas em qualquer curso de cálculo, a derivada de uma constante é zero, de forma que há infinitas funções que satisfazem nossas condições de contorno. Apenas para exemplo, no gráfico a seguir, vemos 5 das antiderivadas de 2x.
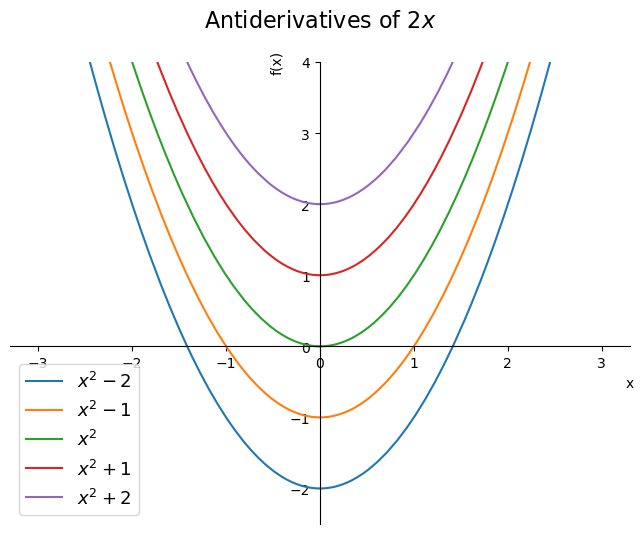
O código para este gráfico está neste meu repositório.
Integral como uma soma de elementos infinitesimais
A abordagem anterior é a matemática, a que permite que saibamos como obter uma expressão para uma integral e a que dá origem às regras que aprendemos em cursos de cálculo. Mas qual o significado de uma integral?
Considere que nossa função de interesse é
f(x) = \frac{1}{x^2 + 1}Com base em qualquer tabela de integrais, você verá que
\int \frac{1}{x^2 + 1} dx = \arctan(x) + CE, com um pouco de SymPy que vimos no artigo sobre gráficos, podemos obter o gráfico da função para um determinado domínio:
from sympy import Symbol, plot
x = Symbol('x')
expr = 1 / (x**2 + 1)
plot(expr, (x, -0.5, 5.5));A integral que obtivemos é chamada de indefinida, pois não especificamos os limites de integração. Caso os limites de integração sejam especificados, a integral passa a se chamar definida e podemos obter um valor. Por exemplo,
\int_0^5 \frac{1}{x^2 + 1} dx = \arctan(5) - \arctan(0) = \arctan(5) \approx 1.3734Poderíamos destacar essa região entre os limites de integração no gráfico, pintando a região:
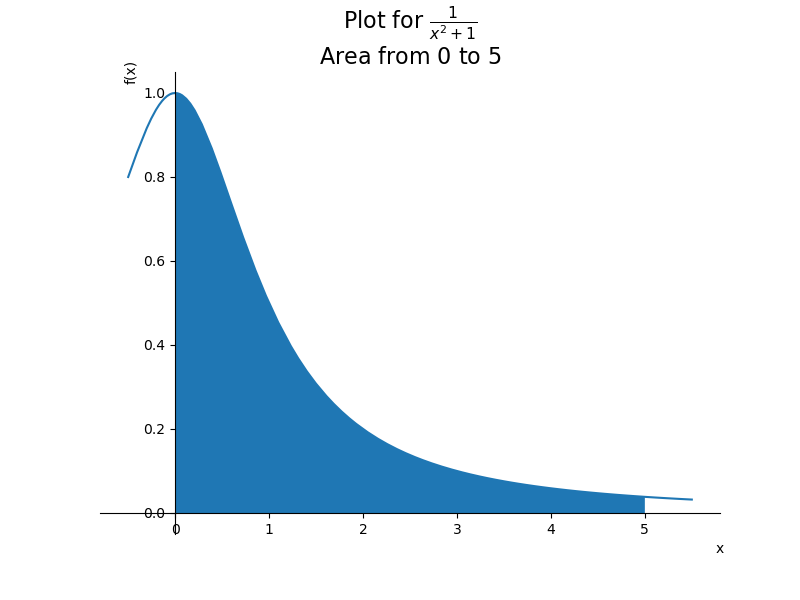
E… é esse o significado de integral, mais especificamente uma integral definida! É a área da região entre o gráfico e o eixo horizontal do plano.
Agora que temos um significado gráfico, é fácil estender para um significado físico. Por exemplo, se o eixo vertical for a pressão sobre um gás e o horizontal for a variação de volume do gás, a área é simplesmente o trabalho exercido sobre o gás. Por isso em disciplinas de física e engenharia há um grande interesse em áreas de gráficos.
OK, quando temos o gráfico é relativamente fácil de enxergar o significado. Mas, como obter um valor? Afinal, para figuras geométricas simples, como retângulos, triângulos e círculos, aprendemos fórmulas para calcular área nas disciplinas de matemática básica. Mas, e a área de uma região como a do gráfico acima? Como uma calculadora ou um computador fazem para apresentar um valor para você?
Ora, sabemos calcular a área de, por exemplo, um retângulo. Vamos colocando retângulos lado-a-lado tentando imitar o melhor possível o formato do gráfico. Sim, é sério. É essa a ideia da chamada soma de Riemann. Veja na animação a seguir como que usando retângulos cada vez menores temos uma aproximação cada vez melhor de nossa integral:
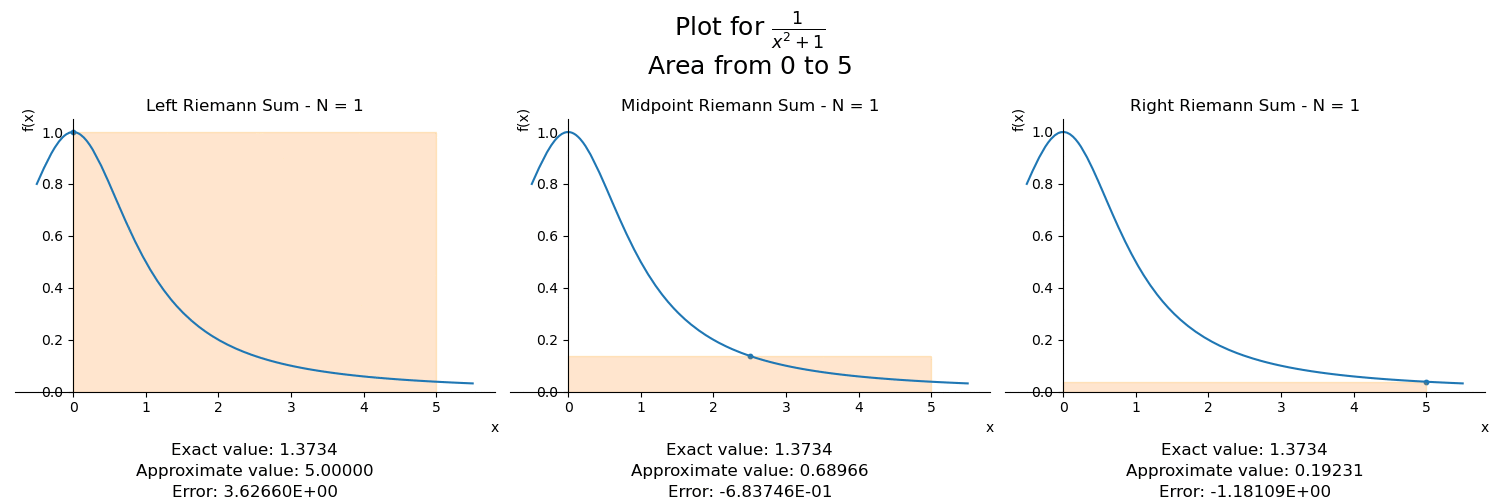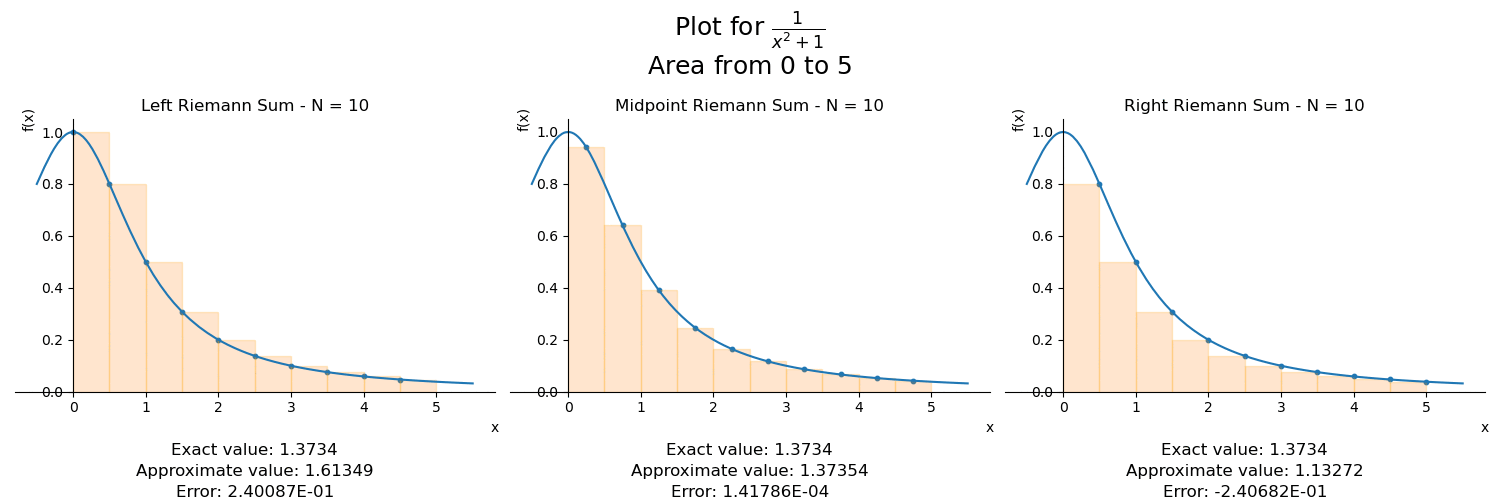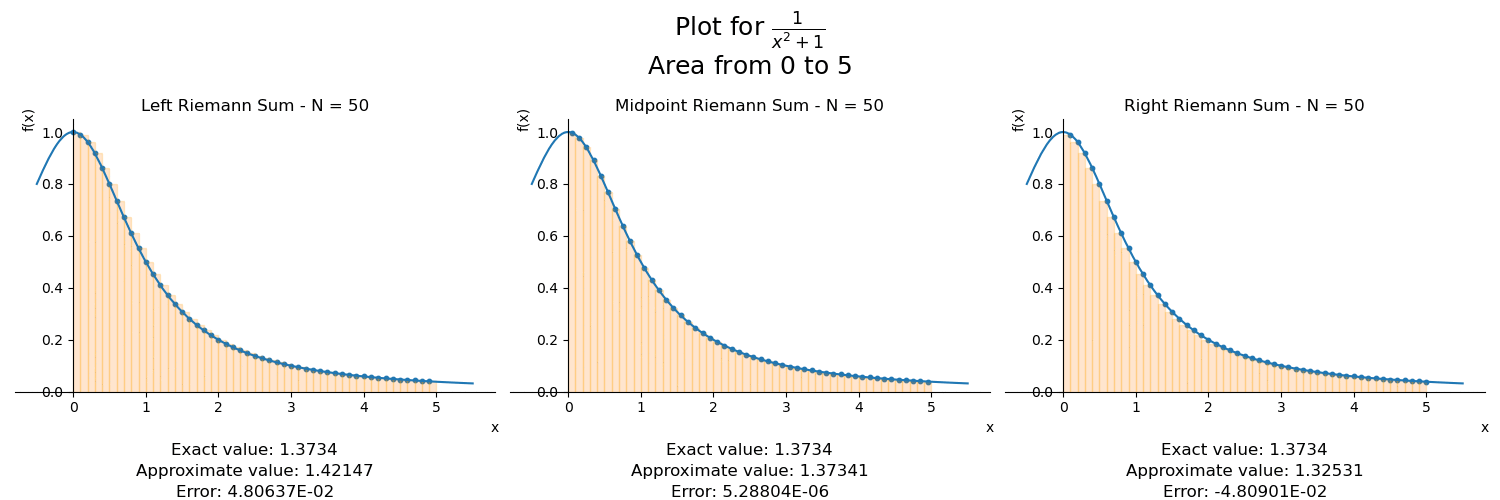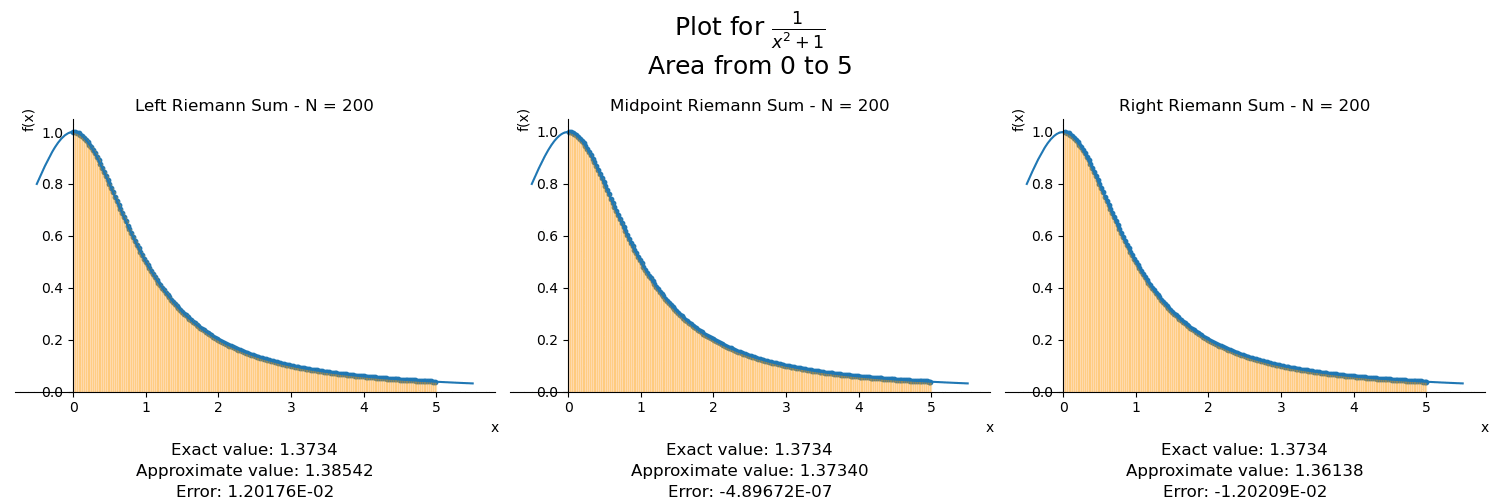
Vemos três gráficos na figura. Quando decidimos a quantidade de subintervalos na qual dividiremos nosso intervalo, podemos alinhar os retângulos nos extremos esquerdo ou direito de cada subintervalo, ou no meio do intervalo. Por isso temos três gráficos.
Gostou da animação? Aqui está o repositório com o código. Quer saber como fazer animações com Python? Me conta nos comentários abaixo do artigo ou nas redes sociais do Ciência Programada. Quem sabe não vira artigo futuro aqui?
Ou seja, os valores que calculadoras ou programas de computador retornam para integrais são resultados de aproximações numéricas. Com base nesse raciocínio, há outros métodos de aproximação como a regra do trapezoide ou as regras de Simpson. Geralmente essas aproximações numéricas são vistas em disciplinas de Cálculo Numérico.
OK, e o Python?
Integrais com SymPy
Vamos criar essa mesma função que usamos como exemplo com o SymPy, aproveitando para importar outras funções que usaremos mais adiante:
# configuração para outputs melhores no artigo, pode ser ignorado
from sympy import init_printing
init_printing(use_latex='png', scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
from sympy import integrate, Symbol, dsolve, Function, diff, Eq
x = Symbol('x')
expr = 1 / (x**2 + 1)
exprPara obter a integral indefinida da função, basta passar sua expressão expr para a função integrate:
integrate(expr, x)Mesmo resultado que apareceu no texto anteriormente exceto por um detalhe… cadê a constante de integração?
O SymPy “simplifica” o resultado, omitindo a constante de integração, de forma a facilitar a passagem do resultado para outras funções do SymPy caso desejado. No entanto, devemos estar conscientes que ela existe. Ou podemos forçar seu aparecimento 🙂
Vimos anteriormente que podemos interpretar uma integral como uma antiderivada, que nada mais é que uma função que é igual a uma determinada derivada. Ora, temos então uma equação diferencial, e já vimos como resolver equações diferenciais com o SymPy.
Vamos criar nossa função que buscamos e criar nossa equação:
F = Function('F')
eqdif = Eq(diff(F(x)), expr)
eqdifLogo, a função que buscamos (e que é a integral desejada) é:
dsolve(eqdif, F(x))Aí está a constante de integração 😉
Veja a importância de saber os fundamentos do que se está fazendo. Infelizmente, muitos docentes têm certo receio de apresentar ferramentas computacionais no ensino por achar que os alunos vão usar e não vão aprender a fazer as contas “na mão”. Da mesma forma, vários estudantes acham perda de tempo fazer manualmente o que um computador faz em questão de segundos. A questão é que o computador só faz o que é solicitado. Se você não sabe o que solicitar…
Além disso, a análise crítica do resultado cabe ao usuário. A ausência da constante de integração no retorno da integrate foi uma escolha dos desenvolvedores, mas a percepção de que ela estava faltando deve ser do usuário, com base em seus conhecimentos de cálculo. É de se esperar que tudo que foi apresentado aqui em termos de cálculo seja de conhecimento de quem fez um curso de cálculo básico.
Assim, com esse exemplo bem simples envolvendo uma simples constante de integração, espero que tanto docentes quanto discentes tenham consciência de que o conhecimento básico do assunto ainda é necessário ao se utilizar programação.
Continuando…
E integrais definidas? Simples, passamos um segundo argumento para integrate com o símbolo da variável e o intervalo desejado:
integrate(expr, (x, 0, 5))Se quisermos uma aproximação numérica, podemos utilizar o método evalf que já vimos em outro artigo:
integrate(expr, (x, 0, 5)).evalf()Aliás, a documentação do método possui uma parte dedicada apenas aos algoritmos de aproximação utilizados em integrais. Se você gostou do início do artigo sobre o método de Riemann, talvez tenha interesse em ler a documentação.
Falando em métodos de aproximação…
Integrais com SciPy
Temos escrito muito sobre o SymPy aqui no site, tendo uma categoria apenas para ele. O grande poder do SymPy é o fato de ele ser uma biblioteca simbólica, de forma que podemos inserir e obter resultados de uma forma muito similar a que estamos acostumados em materiais do nosso cotidiano, como livros. Você deve ter percebido isso ao ler o artigo, as notações utilizadas muito se aproximam das vistas em livros e artigos. O próprio resultado da integral definida ser apresentado como atan(5) ao invés de seu valor numérico aproximado é bem característico de uma biblioteca simbólica.
Do meu ponto de vista, é muito útil iniciar o estudo de Python científico por uma biblioteca simbólica, daí a quantidade de artigos que escrevo sobre. É bem mais simples criar os símbolos e manipulá-los como em uma disciplina normal de matemática ou afins, sem a necessidade de ficar criando listas ou arrays de números e funções.
No entanto, tudo tem seus prós e contras. O SymPy pode ser relativamente lento se utilizado para obter valores numéricos de contas muito extensas. E não tem foco em aproximações numéricas, não tendo muitas ferramentas nesse sentido. Daí a existência do NumPy e de bibliotecas construídas sobre ele, como o SciPy. Vamos usar este último agora.
A forma mais fácil de obter o SciPy é através do pacote Anaconda, que já vimos aqui no site.
Ah, já mostramos o SciPy aqui antes quando calculamos a velocidade do atleta Usain Bolt com Python. Recomendo a leitura 😉
O SciPy é dividido em subpacotes que cobrem diferentes domínios de conhecimento. No subpacote integrate, destinado a problemas envolvendo integrais e equações diferenciais, há o método quad. quad vem de quadratura, um termo histórico que se refere a integrais.
Podemos passar uma função e os limites de integração e obter uma aproximação numérica do resultado:
from scipy.integrate import quad
def exemplo(x):
return 1 / (x**2 + 1)
quad(exemplo, 0, 5)Veja que foi retornada uma tupla. O primeiro valor é a aproximação desejada; o segundo é uma estimativa do erro desta aproximação. O valor obtido para a aproximação é igual ao exibido pelo SymPy anteriormente quando solicitamos uma aproximação numérica. Mas, o algoritmo interno do quad é distinto do usado pelo SymPy, sendo o de Clenshaw-Curtis.
Observe que quando foi escrito acima que podemos passar uma função, “função” é efetivamente uma função do Python e não função no sentido matemático, como quando usávamos o SymPy. No SymPy, criávamos uma variável que representa uma função matemática, deixando tudo mais fluido. Aqui, com o SciPy, precisamos criar uma função do Python que representa a ideia de função matemática. Cuidado com a compreensão da mesma palavra em contextos distintos para não se confundir.
Mas, vamos lembrar da variável que representava a nossa função lá no SymPy:
exprPor padrão, objetos do SymPy não se comunicam com objetos do SciPy. Porém, o SymPy possui a função lambdify que permite fazer a transformação de objetos SymPy em objetos que podem ser entendidos pelo SciPy e pelo NumPy. Passamos o símbolo utilizado no objeto e o objeto SymPy em si:
from sympy import lambdify
f = lambdify(x, expr)
f<function _lambdifygenerated(x)>
type(f)function
Veja que o retorno é um objeto tipo função. Vamos passá-lo para quad:
aprox_quad = quad(f, 0, 5)
aprox_quadObtivemos o mesmo resultado. O lambdify é absurdamente útil nesta transição simbólico -> numérico.
Escrevi acima que há diversos métodos de aproximação no SciPy. No início do artigo, vimos a soma de Riemann, mostrando a ideia de retângulos cada vez mais estreitos se aproximando da área da curva. E citei outros métodos de aproximação: trapezoidal e Simpson. Vejamos a implementação desses métodos com o SciPy.
Começando pelo trapezoidal. A ideia é a mesma da vista na animação de Riemann, mas ao invés de retângulos, se usam trapézios. Assim, precisamos de pontos que serão utilizados como vértices desses trapézios. Vamos começar criando 10 valores para x e seus correspondentes para a função. Usaremos o linspace do NumPy para gerar 10 valores igualmente espaçados entre nossos limites de integração 0 e 5:
import numpy as np
x = np.linspace(0, 5, 10)
x, f(x)(array([0. , 0.55555556, 1.11111111, 1.66666667, 2.22222222,
2.77777778, 3.33333333, 3.88888889, 4.44444444, 5. ]),
array([1. , 0.76415094, 0.44751381, 0.26470588, 0.16839917,
0.11473088, 0.08256881, 0.06202144, 0.0481856 , 0.03846154]))
Agora, veremos a estimativa dada pelo método trapezoid do SciPy:
from scipy.integrate import trapezoid
aprox_trap = trapezoid(f(x), x)
aprox_trapVamos ver a diferença entre o valor obtido por esse método e o obtido pelo método quad:
aprox_trap - aprox_quad[0]Vemos que, mesmo com apenas 10 pontos intermediários, a diferença está apenas a partir da quarta casa decimal. E se tivermos mais pontos?
pontos = (5, 10, 20, 50, 100, 200)
print('Aproximação Diferença p/ quad')
for quantidade in pontos:
x = np.linspace(0, 5, quantidade)
aprox_trap = trapezoid(f(x), x)
print(aprox_trap, aprox_trap - aprox_quad[0])Aproximação Diferença p/ quad 1.3922446845579102 0.018843917612893613 1.3730596135430173 -0.00034115340199925015 1.3733154390709228 -8.532787409376574e-05 1.3733879321834697 -1.2834761546898221e-05 1.3733976225738 -3.1443712165124538e-06 1.3733999887221857 -7.782228308439443e-07
Como esperado, quanto mais pontos, menor a diferença entre os métodos. Como a aproximação dada por quad utiliza uma forma de cálculo mais elaborada, podemos tomá-la como referência.
O método simpson segue a mesma lógica, mas usando a regra de Simpson citada anteriormente:
from scipy.integrate import simpson
print('Aproximação Diferença p/quad')
for quantidade in pontos:
x = np.linspace(0, 5, quantidade)
aprox_simpson = simpson(f(x), x)
print(aprox_simpson, aprox_simpson - aprox_quad[0])Aproximação Diferença p/quad 1.3086914096492739 -0.06470935729574268 1.3625908639477373 -0.010809902997279242 1.3719873244581011 -0.0014134424869154394 1.3733135225951851 -8.724434983142793e-05 1.3733901045694628 -1.0662375553804893e-05 1.3733994515711914 -1.3153738251947544e-06
Assim, da mesma forma, a diferença diminui quanto mais pontos são fornecidos.
Conclusão
Espero que o artigo tenha te ajudado a revisar cálculo e a integrar os conhecimentos matemáticos com os de programação Python. E, mais, que tenha te despertado para o fato de que quase todo valor apresentado por um programa é fruto de aproximações. Esquecer desse fato pode levar a problemas. Não por acaso, chamo atenção para aproximações com uma certa frequência nos artigos.
Acompanhe o projeto Ciência Programada nas redes sociais para saber quando são publicados novos artigos, em breve escreverei mais sobre cálculo 😉
A lista completa de artigos sobre SymPy pode ser vista na categoria SymPy aqui do site.
Até a próxima.





Gostaria de aprender a fazer animações em Python!
Bom dia, Pedro
Devo fazer material sobre animações em algum momento em breve. Há alguns links para exemplos na documentação do Matplotlib: https://matplotlib.org/stable/api/animation_api.html
Abraço