Engenheiros e cientistas sempre buscam extrair o máximo de desempenho de seus equipamentos e projetos com o mínimo de custo. Essa busca dá origem aos chamados problemas de otimização. Neste artigo, veremos como podemos utilizar a linguagem Python, com auxílio do pacote SymPy, na resolução de tais problemas.
Tópicos
Entendendo um problema de otimização
Comecemos entendendo a essência de um problema de otimização do ponto de vista matemático. Podemos entender otimização como sendo a busca por uma entrada para uma função f(x) tal que o resultado seja o melhor valor de saída para a f(x). E o que seria esse “melhor valor”? Geralmente, significa o valor máximo (se a função representa algo positivo como, por exemplo, lucro), ou o valor mínimo (se a função representa algo indesejado, como custo).
No artigo sobre derivadas com Python, vimos que a derivada de uma função possui relação com a inclinação de uma reta tangente à função em um dado ponto. Assim, quando f'(x) = 0, tal inclinação é nula indicando que se está em um ponto de máximo ou de mínimo. Pontos que satisfazem a igualdade anterior são chamados pontos críticos de uma função.
Já a derivada segunda, f''(x), tem relação com a curvatura de f(x) e podemos a utilizar para verificar se um dado ponto crítico é de máximo ou de mínimo. Se f''(x) < 0, a função é um máximo; se f''(x) > 0, a função é um mínimo; já se f''(x) = 0, a função está em um ponto de inflexão, mudando de uma região de máximo para uma de mínimo, ou vice-versa.
Vamos partir para um exemplo. Considere a seguinte função:
f(x) = x^3 - 2x^2 + xVamos criá-la com o SymPy:
# configuração para outputs melhores no artigo, pode ser ignorado
from sympy import init_printing
init_printing(use_latex='png', scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
# importando o necessário para este início de artigo
from sympy import Symbol, diff, solve, plot
# criando o símbolo da variável e a função
x = Symbol('x')
f = x**3 - 2*x**2 +x
fPodemos facilmente com a função diff do SymPy obter as derivadas primeira e segunda:
derivada_primeira = diff(f, x)
derivada_primeiraderivada_segunda = diff(f, x, 2)
derivada_segundaCom a função solve, podemos obter os pontos críticos resolvendo a primeira derivada para x. Ou seja, resolvendo f'(x)=0:
pontos_criticos = solve(derivada_primeira, x)
pontos_criticosObserve que o resultado sai em forma de uma lista. Podemos substituir cada resultado obtido na expressão da derivada segunda:
derivada_segunda.subs({x: pontos_criticos[0]}), derivada_segunda.subs({x: pontos_criticos[1]})E verificar se há algum ponto de inflexão:
ponto_inflexao = solve(derivada_segunda, x)
ponto_inflexaoVemos que f''(\frac{1}{3}) < 0, indicando ser um ponto de máximo, e que f''(1) > 0, sendo um ponto de mínimo. Em x = \frac{2}{3} há mudança de concavidade da função.
Vejamos o gráfico da função:
plot(f, (x, -0.2, 1.2));Veja que o gráfico foi propositalmente construído em um intervalo (domínio) tal que fica evidente o máximo e o mínimo. No entanto, observe que a função é crescente para x > 1 e decrescente para x < 0. Daí a importância de se definir um domínio de validade para o problema logo no início. Supondo um domínio tal que x \in [0, 1] podemos afirmar que (\frac{1}{3}, f(\frac{1}{3})) é um ponto de máximo.
Exemplo de aplicação – minimizando custos
Vamos pegar um exemplo bem comum em processos químicos: a minimização do custo de construção de um tanque. Aliás, sou químico de formação, já escrevi aqui um pouco de como a tecnologia influenciou minha carreira, assim como certamente influencia a sua, e há artigos na tag química aqui do site mostrando como aplicar programação em química. Para mais detalhes de meus projetos, veja meu portfolio.
Obtendo nossa função
Em nosso exemplo, consideraremos um tanque cilíndrico de volume fixo (V) e desejamos determinar o comprimento (L) e o diâmetro (D) que minimizam o custo do tanque. O custo por unidade de área da lateral do tanque é c_s e o custo por unidade de área do topo e do fundo do tanque é c_t. Com um pouco de geometria básica apresentada na figura a seguir, conseguir obter nossa função f que representa o custo:
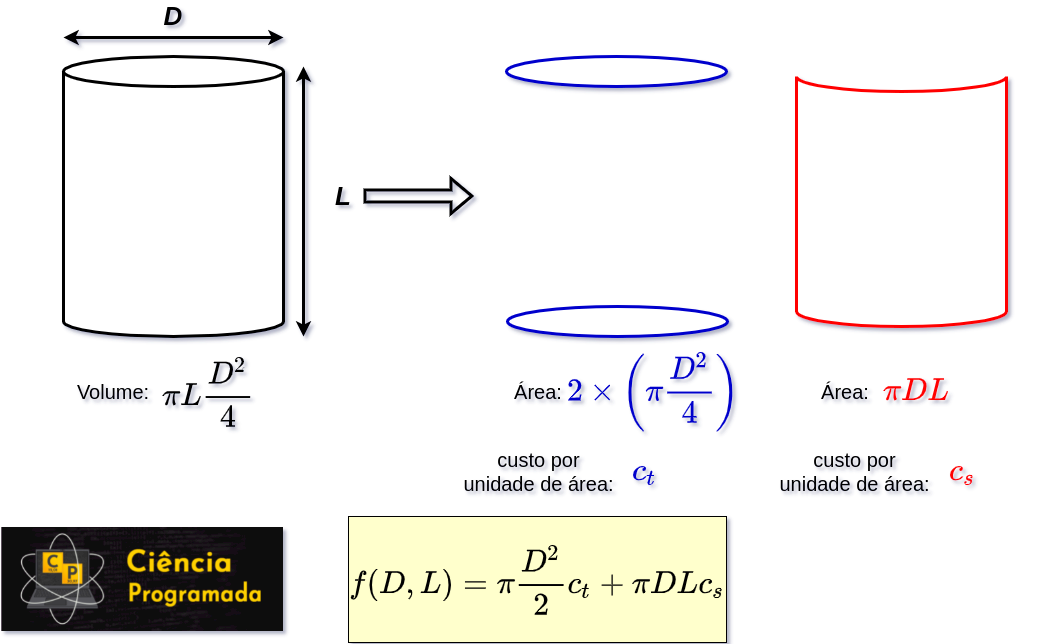
Vamos criar os símbolos necessários para representar nossa função. Observe que em todos foi colocada a restrição de que são valores positivos, já que não faz sentido falar em dimensões ou custos negativos. É importante lembrar de avaliar restrições em problemas de otimização.
from sympy import pi
diametro = Symbol('D', positive=True)
comprimento = Symbol('L', positive=True)
volume = Symbol('V', positive=True)
custo_lado = Symbol('c_s', positive=True)
custo_topo = Symbol('c_t', positive=True)
f = custo_lado * pi * diametro * comprimento + custo_topo * (pi / 2) * diametro**2
fVamos considerar que não há limite para os valores e buscar uma expressão em função de V e de D. Assim, eliminando L da expressão:
volume_cilindro = (pi / 4) * diametro**2 * comprimento
volume_cilindrocomprimento_funcao_volume = solve(volume_cilindro - volume, comprimento)[0]
comprimento_funcao_volumef = f.subs({comprimento: comprimento_funcao_volume})
fLogo, a expressão acima é a que queremos otimizar, obtendo um valor mínimo. Vamos obter a expressão de sua derivada primeira em relação ao diâmetro:
f_min = diff(f, diametro)
f_minAgora, podemos obter uma expressão para o diâmetro que torna a derivada nula:
diametro_otimo = solve(f_min, diametro)[0]
diametro_otimoE, com o diâmetro, obter o comprimento otimizado:
comprimento_otimo = comprimento_funcao_volume.subs({diametro: diametro_otimo}).simplify()
comprimento_otimoVejamos qual a razão comprimento / diâmetro que minimiza o custo:
comprimento_otimo / diametro_otimoVeja que resultado interessante. Se os custos forem os mesmos, o cilindro que minimiza o custo é aquele que possui comprimento igual ao diâmetro da base, já que a razão acima teria valor 1. Escreveremos mais sobre isso adiante.
Vamos colocar valores de exemplo para visualizar melhor nosso resultado. Vamos considerar os custos iguais a 1 unidade e o volume igual a 10 unidades. O diâmetro que minimiza a função é:
solve(f_min.subs({custo_lado: 1, custo_topo: 1, volume: 10}), diametro)[0]Que, numericamente, corresponde a:
# o _ permite recuperar o valor da célula anterior
_.n()Vejamos o gráfico de nossa função custo:
p = plot(f.subs({custo_lado: 1, custo_topo: 1, volume: 10}),
(diametro, 0, 5), ylim=(0, 100), legend=True, show=False)
p[0].label = 'f'
p.show()Veja como realmente há um mínimo ao redor do diâmetro 2,33. Logo, este é o diâmetro (e também o comprimento) para as condições de contorno fornecidas.
E se os custos forem distintos?
O que acontece se os custos forem distintos? Vamos considerar o custo da lateral do tanque como o dobro do custo de topo:
solve(f_min.subs({custo_lado: 2, custo_topo: 1, volume: 10}), diametro)[0]_.n()Veja que o diâmetro da base aumentou comparado ao caso anterior. Consequentemente, como a razão comprimento / diâmetro depende apenas dos custos, o comprimento é metade do diâmetro obtido. Consegue agora entender o formato “achatado” dos cilindros que armazenam líquidos que costumamos ver em plantas industriais?
Nesses cilindros a pressão interna do líquido é dada pela famosa equação P = \rho g h, ou seja, depende da densidade do líquido, da gravidade e da altura da coluna de líquido. Logo, um tanque alto levaria à necessidade de se ter paredes mais grossas para aguentar a pressão do líquido. E, claro, isso afeta muito os custos de construção, especialmente das paredes laterais. Simples, não? Claro que há muito mais envolvido, como pode ser visto aqui.
E todos esses formatos diferentes para latas de alimentos?
Vimos nas contas acima que, se os custos da lateral e do topo forem iguais, o formato cilíndrico que minimiza o custo total é aquele com diâmetro da base igual ao comprimento do cilindro. Mas, então, por que tal formato é tão raro em enlatados que vemos no mercado? Aliás, primeiramente, por que cilindro?
Em nossas contas, consideramos implicitamente que o custo decorre apenas da área. Logo, por que então não usar recipientes esféricos? Afinal, uma das primeiras coisas ensinadas em aulas de geometria é que a esfera tem a menor área superficial dentre todas as formas fechadas ao redor de um volume. OK, legal… Agora tente empilhar diversos recipientes esféricos em uma prateleira de mercado. Boa sorte 🙂

Além do fato de que esferas rolam muito facilmente, seu empacotamento é pouco efetivo. No máximo conseguimos ocupar 74 % do espaço disponível empilhando esferas. Procure seu químico de confiança mais próximo se quiser uma demonstração matemática disso. Assim, fica claro que outras considerações estão envolvidas no assunto. Não é apenas o custo de construção, há também o de transporte, armazenamento e disposição. Nesse sentido, formatos mais cilíndricos acabam sendo mais interessantes. Além do fator ergonômico, seu cliente precisa ser capaz de segurar o que vai consumir. Já pensou ter que segurar uma latinha de refrigerante com as duas mãos por ter um diâmetro grande?
No processo de manufatura de latas, o maior desperdício é no topo e no fundo pela necessidade de cortes e solda. Claro que há reciclagem, mas isso faz com que o custo seja distinto, sendo que nesse caso o custo da lateral é menor fazendo sentido latas mais altas.
Conclusão
Além de cálculo e programação, também tivemos um curso rápido sobre embalagens 😉
Vimos os cuidados que devem ser tomados em problemas de otimização, desde a correta identificação do domínio, passando pelas condições de contorno e análise crítica dos resultados obtidos. E todo o processo foi bem ágil pelo uso do SymPy.
Acompanhe o projeto Ciência Programada nas redes sociais para saber quando são publicados novos artigos, em breve escreverei mais sobre cálculo 😉
A lista completa de artigos sobre SymPy pode ser vista na categoria SymPy aqui do site.
Até a próxima.




