Um bom tempo do estudo de cálculo é destinado às chamadas séries infinitas. Mas, afinal, o que são séries infinitas? E qual sua relação com o paradoxo de Aquiles e a tartaruga, um dos chamados paradoxos de Zenão de Eleia, filósofo grego? Qual a relação com quântica e o princípio da incerteza? E onde entra Python nisto tudo? É o que descobriremos neste artigo.
Tópicos
Aquiles e a tartaruga
Aquiles, herói grego, e uma tartaruga disputam uma corrida. Como a velocidade de Aquiles é maior que a da tartaruga, esta recebe uma vantagem, começando a corrida um trecho na frente da linha de largada de Aquiles. Aquiles nunca sobrepassa à tartaruga, pois quando ele chegar à posição inicial A da tartaruga, esta encontra-se mais a frente, numa outra posição B. Quando Aquiles chegar a B, a tartaruga não está mais lá, pois avançou para uma nova posição C e assim sucessivamente, ad infinitum.

Esse é um dos chamados paradoxos de Zenão de Eleia (c. 495 – c. 430 BC), filósofo grego. Claramente, sabemos que Aquiles passará a tartaruga, por uma simples questão de vivência prática. Mas você consegue achar as falhas no texto acima? E, especialmente, consegue formular o problema matematicamente?
Zenão era um eleático. A escola filosófica eleática rejeitava a validade de experiências sensoriais e materiais, considerando que apenas lógica deveria ser critério para a verdade. Os eleáticos se baseavam no conceito de unidade universal e que experiências sensoriais não são coerentes com essa unidade por serem inconsistentes e, por vezes, contraditórias. Apenas o pensamento poderia superar falsas aparências sensoriais e chegar ao conhecimento do ser, à verdade fundamental de “tudo é um”. E mais, não pode haver criação, pois o ser não pode vir do não-ser, visto que uma coisa não pode surgir de algo que é diferente.

Aham, bem alucinógena curiosa a forma de pensar. Não vou prosseguir nesta viagem nos pormenores da escola, deixo isso para os filósofos. Porém, a última frase leva à ideia de que mudanças são apenas uma ilusão dos sentidos, sendo o movimento igualmente uma ilusão, uma falsa aparência de mutabilidade, contrária à unicidade universal. Daí o surgimento do paradoxo para Zenão. Vamos para uma visão mais matemática.
Séries infinitas, o conceito de limite e solução do paradoxo
O paradoxo, em seu cerne, esconde a ideia de infinito, concorda? Conforme descrito anteriormente em seu enunciado, poderíamos continuar expandindo para outras posições: D, E, F… indefinidamente. A ideia de infinito não é nem um pouco trivial e já a abordamos brevemente em outros artigos, para ver como era representada em pacotes Python como o SymPy.
Outra ideia que, por muitos séculos, foi considerada não trivial e paradoxal é a de que uma soma infinita pode produzir um resultado finito. Tal ideia passou a ser mais fácil de entender no século XVII com o conceito de limite e o trabalho de Augustin-Louis Cauchy. Vejamos um de seus estudos:
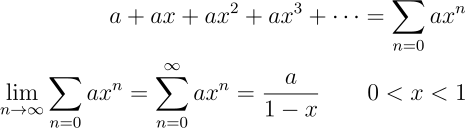
Na primeira linha, expressamos a ideia de uma soma infinita pelo símbolo de somatório. Na segunda, pegamos esse somatório e colocamos um limite tendendo ao infinito para n, aproveitando para expressar tal limite acima do símbolo de somatório. E, para a condição de 0 < x < 1, é possível obter uma expressão para o limite. Ou seja, o limite, que é para uma soma infinita, converge para um valor finito quando esta condição é obedecida. Daí o estudo de convergência de séries tão comum em disciplinas de cálculo. Voltaremos a esse assunto mais adiante no artigo.
Mas o que isso tem a ver com nosso paradoxo?
Para começar, vamos colocar algumas condições de contorno em nosso problema:
- Aquiles começa em uma posição inicial x_A
- Tartaruga começa em uma posição inicial x_T
- Aquiles possui uma velocidade constante v_A
- Tartaruga possui uma velocidade constante v_T
Ora, a variação da posição, x, de ambos com o tempo, t, pode ser expressa por equações de movimento uniforme estudadas em física:
x(t) = x_0 + vtonde x_0 é a posição inicial de cada um e v a velocidade constante de cada um.
O que buscamos? Bom, sabemos que, para Aquiles ultrapassar a tartaruga, em alguma posição os dois estarão lado-a-lado. Em quanto tempo isto ocorrerá?
Se temos as equações de posição de ambos, podemos igualá-las e resolver para a variável tempo. Basta resolver uma equação simples, o que já vimos em artigos anteriores com o SymPy. Comecemos importando o necessário, criando nossos símbolos e achando a igualdade que representa a posição de encontro de ambos:
# configuração para outputs melhores no artigo, pode ser ignorado
from sympy import init_printing
init_printing(use_latex='png', scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
from sympy import S, symbols, Eq, solve
xA, xT, vA, vT, t = symbols('x_A x_T v_A v_T t')
posicao_encontro = Eq(xA + vA * t, xT + vT * t)
posicao_encontroCom a função solve, podemos obter a expressão para o tempo em que tal encontro ocorrerá:
tempo_encontro = solve(posicao_encontro, t)[0]
tempo_encontroVamos agora colocar alguns valores para deixar o assunto mais palpável. Vamos considerar que:
- à tartaruga foi dada uma vantagem inicial de 100 m
- a velocidade de Aquiles é 10 m/s
- a velocidade da tartaruga é 1/10 m/s
Os valores podem ser outros, escolhi esses apenas por serem mais fáceis de fazer conta mentalmente. Substituindo na expressão de tempo obtida, vemos que, com um mínimo de manipulação, obtemos uma expressão compatível com a fórmula obtida para o limite mostrado anteriormente:
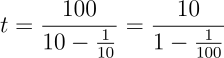
Ou seja, o tempo pode ser expresso pela seguinte série infinita:
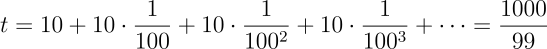
Substituindo os valores na expressão do SymPy, obtemos o mesmo valor:
tempo_encontro.subs({xA: 0, xT: 100, vA: 10, vT: S('1/10')}) # segundosPodemos, com o método n, ter uma aproximação numérica do tempo necessário, em segundos, para nosso exemplo:
tempo_encontro.subs({xA: 0, xT: 100, vA: 10, vT: S('1/10')}).n() # segundosSe temos uma resposta, onde está o erro de Zenão? Bom, há diversas abordagens, mas em nossas contas o que fica mais evidente é que Zenão não considerou o tempo. Como as velocidades são distintas, o tempo que Aquiles levará em cada trecho é diferente do tempo que a tartaruga levará, fazendo com que eventualmente ele alcance, e ultrapasse, a tartaruga. Basta observar na série que cada termo é um incremento menor de tempo. Lembre-se: estamos falando de milênios atrás, conceitos como velocidade ainda não eram formalmente definidos. O erro no enunciado de Zenão é a palavra “nunca”, que implica tempo, enquanto que todo o enunciado é formulado em termos de distância percorrida. Também há a constante mudança de sistema de referência: Aquiles -> tartaruga -> Aquiles… que leva à impressão de recomeço em cada ponto. Quando colocamos a referência fixa, como quando definimos as equações de movimento uniforme, esta impressão se desfaz.
Outra coisa importante a se reparar é que não é necessária a noção de série infinita e nem de limite para a resolução do paradoxo. As equações simples de movimento uniforme bastam. No entanto, a formulação do raciocínio via incrementos de tempo leva a importantes considerações que utilizam conceitos que levaram séculos para serem bem definidos e sedimentados.
Vamos explorar mais a ideia de séries infinitas no SymPy.
Representando séries infinitas no SymPy
Vamos tentar reconstruir o somatório visto no exemplo do paradoxo. O SymPy tem a classe Sum que permite criar um somatório:
from sympy import Symbol, oo, Sum, summation
# sempre que possível, expresse as restrições de seus símbolos
# aqui, irei considerar as restrições de nosso exemplo anterior
a = Symbol('a', positive=True)
n = Symbol('n', positive=True)
x = Symbol('x', positive=True)
expr = a * x**n
s = Sum(expr, (n, 0, oo))
sVeja que, de forma bem simples, criamos nosso somatório! Porém, mais do que criar, seria interessante ser capaz de obter resultados simbólicos para o mesmo. Para isso, temos o método doit (literalmente, “faça!”)
s.doit()Caso queira pular a etapa de criar o somatório e mandar fazê-lo diretamente, há a função summation que faz tudo em uma única etapa:
s = summation(expr, (n, 0, oo))
sVeja que interessante. A resposta considera duas situações, uma com x<1 e outra onde não há esta condição. Quando x<1 (e maior que zero, premissa omitida por ter sido definida na criação do símbolo com positive=True), temos exatamente a expressão esperada de acordo com o que vimos na seção anterior. Para demais valores de x não há convergência, de forma que o SymPy apenas deixa a expressão indicada.
Vamos, então, substituir os valores de exemplo utilizados na seção anterior:
s.subs({a: 10, x: S('1/100')})Como esperado, mesmo valor de nossas contas prévias. Podemos solicitar uma aproximação numérica:
s.subs({a: S('10'), x: S('1/100')}).n()Este é o poder de uma biblioteca simbólica. Veja como, por diferentes caminhos, obtivemos o mesmo resultado com poucos comandos. Comandos estes que abstraem conceitos bem elaborados, como o de uma equação ou o de uma série infinita.
Entendendo a importância prática de séries infinitas
A história do paradoxo serviu para introduzir a ideia de séries infinitas de uma forma mais amigável. Mas qual a real aplicação delas?
Um dos artigos que deu mais trabalho eu mais gostei de escrever foi o sobre integrais. Em tal artigo, mostro que é importante ter a noção de que muito do que calculadoras, planilhas e funções matemáticas de linguagens de programação apresentam para você são frutos de aproximações numéricas. Por exemplo:
from sympy import exp
exp(5)Veja que o SymPy deixou indicada a exponencial. Podemos solicitar um valor numérico:
exp(5).n() # equivalente a exp(5).evalf()Como o SymPy obtém tal valor? Usamos como exemplo a função exponencial, mas o mesmo questionamento se aplica às funções trigonométricas ou, de forma mais genérica, a funções transcendentes.
Do ponto de vista computacional, tudo tende a ser reduzido a operações mais simples, como adições e multiplicações, já que são rápidas e há muitas décadas vem sendo otimizadas por softwares e hardwares. Há diversos algoritmos para aproximar funções como o CORDIC, algoritmos baseados em polinômios de Chebyshev, e baseados em séries de Taylor, apenas para citar alguns exemplos. Na prática, pode se utilizar uma combinação de diversos algoritmos a depender da entrada da função e do domínio da mesma. E, ainda, qual implementação será utilizada pode mudar a depender do hardware, como discutido neste link do StackOverflow.
Vemos, portanto, que é um assunto bem extenso. Neste artigo, vamos primeiro falar da série de Taylor. Tal série é estudada em cursos introdutórios de cálculo pela simplicidade e diversas bibliotecas matemáticas possuem implementações, como é o caso do SymPy.
Série de Taylor
Considere uma função que pode ser expressa pela série
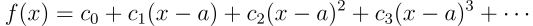
onde a é uma constante, assim como os coeficientes c_i. Assuma que a função tem derivadas contínuas em todas as ordens. Vamos avaliar a função e suas derivadas em x=a:
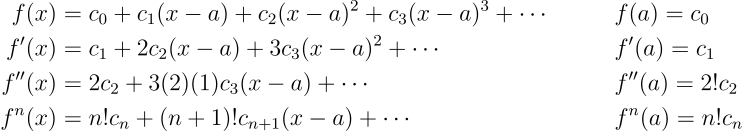
Substituindo os coeficientes em nossa função original:
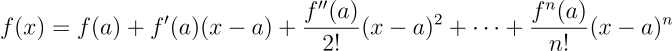
que é a chamada série de Taylor.
No caso específico em que a = 0, temos:
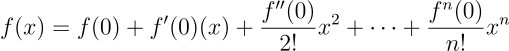
que, em alguns livros, é chamada de série de Maclaurin.
Ora, vamos recriar tudo isso no SymPy, para isso que você está lendo até aqui. O SymPy possui uma função series que faz uma série de Taylor de uma função ao redor de um dado valor. Ela recebe uma função matemática, a variável e o valor. Vamos criar uma função com o SymPy e os símbolos necessários:
from sympy import Function, series
f = Function('f')
a, n, x = symbols('a n x')
series(f(x), x, a)Exatamente o esperado pelo que vimos no decorrer do texto, apenas com uma notação distinta. Repare que o último termo é apresentado com uma notação de Bachmann-Landau, indicando que os demais termos são de ordem 6 em diante. É possível remover essa notação com o método removeO:
series(f(x), x, a).removeO()Passando um número como quarto parâmetro podemos definir qual a ordem máxima da série. Por exemplo, passando 3 como parâmetro:
series(f(x), x, a, 3)Como nossa função possui apenas uma variável, x, podemos omitir sua passagem. Se omitirmos o valor ao redor do qual a expansão em série está sendo feita, subentende-se que o valor é zero. Assim:
series(f(x))Temos a série de Maclaurin para nossa função.
Podemos obter cada termo da série isoladamente como parte de uma tupla com o atributo args:
series(f(x)).argsFunções do SymPy possuem o método taylor_term para o qual passamos qual a ordem do termo desejado e a variável e obtemos a expressão de tal termo:
f(x).taylor_term(2, x)Outra forma de interagir com cada termo de uma série é através do método lseries. Esse método retorna um gerador, como vemos abaixo. Caso não saiba o que é um gerador, veja este artigo sobre geradores.
gen_f_taylor = f(x).lseries()
gen_f_taylor<generator object Expr.series.<locals>.<genexpr> at 0x7f88f1d4e510>
Com a função next do Python podemos verificar cada termo:
next(gen_f_taylor)next(gen_f_taylor)next(gen_f_taylor)Trabalhar com geradores possui diversas vantagens. Podemos usar a função islice da biblioteca itertools presente em instalações padrão do Python. Já escrevemos sobre a islice. Basicamente, temos controle sobre as próximas saídas do gerador, sem necessidade de ficar utilizando a função next seguidamente. Vamos importar a função e verificar seu retorno passando nosso gerador e solicitando as 5 próximas saídas do gerador:
from itertools import islice
islice(gen_f_taylor, 5)<itertools.islice at 0x7f88f2587cc0>
Veja que o objeto gerado pelo islice também é um gerador. Podemos solicitar que o gerador seja consumido completamente passando-o para alguma estrutura de dados como, por exemplo, uma tupla com a função tuple:
tuple(islice(gen_f_taylor, 5))Vamos entender o retorno obtido. Já havíamos começado a consumir o gerador gen_f_taylor, tendo obtido os 3 primeiros termos da série. Quando passamos como parâmetro o valor 5 para o islice obtivemos os 5 termos seguintes. Como é uma série infinita, podemos fazer este procedimento indefinidamente, obtendo quantos termos desejarmos.
Para começar desde o início da série, podemos redefinir nossa variável ou passar diretamente a função com o método lseries:
tuple(islice(f(x).lseries(), 5))Assim, acima, temos os 5 primeiros termos da série.
Caso passemos 2 números para islice teremos os termos desde a posição do primeiro número até a posição do segundo número. Por exemplo, do terceiro ao sétimo termo:
tuple(islice(f(x).lseries(), 3, 7))Assim, temos controle total sobre a forma que consumimos nossa série. Novamente, caso não tenha trabalhado com geradores anteriormente, veja os artigos citados. Busquei ser bem didático nos mesmos, partindo de exemplos bem simples.
Por fim, poderíamos ter o mesmo comportamento de gerador a partir da função series bastando passar n=None como um dos argumentos:
series(f(x), n=None)<generator object Expr.series.<locals>.<genexpr> at 0x7f88f1de1c10>
tuple(islice(series(f(x), n=None), 3))OK, muita letra e número, vamos ver alguns exemplos mais práticos.
Função exponencial
Vamos retomar o exemplo da função exponencial solicitando uma expansão em série de Taylor ao redor de x = 0:
series(exp(x))Veja que, por padrão, a expansão é feita até o termo de ordem 5, deixando explícito que os demais termos são de ordem 6 em diante. Podemos alterar esse termo de maior ordem. Na célula seguinte, passamos a função, a variável, o valor de x ao redor do qual se faz a expansão e o termo de maior ordem:
series(exp(x), x, 0, 8)E, como já visto, podemos remover a indicação de ordem dos demais termos da série:
series(exp(x), x, 0, 8).removeO()Lembrando, a série nada mais é que um somatório infinito. Podemos, olhando o resultado acima, reconhecer a expressão geral do somatório e reproduzir tal expressão com o SymPy:
from sympy import factorial
n = Symbol('n', integer=True) # importante deixar claro que deve ser inteiro
exp_expr = x**n / factorial(n) # verifique que essa é realmente a expressão
sum_exp = Sum(exp_expr, (n, 0, oo))
sum_expConcorda com o resultado?
Agora, podemos solicitar que o SymPy execute o somatório:
sum_exp.doit()Observe que o SymPy reconhece que o resultado de tal somatório é a função exponencial. Lembrando, isso tudo poderia ter sido em uma linha de código com summation:
summation(exp_expr, [n, 0, oo])Voltando ao exemplo exp(5) utilizado anteriormente, vejamos o que obtemos ao solicitar a substituição de x por 5:
summation(exp_expr.subs({x: 5}), [n, 0, oo])Assim, caso solicitarmos uma aproximação numérica vinda do somatório, esta aproximação deve ser igual à obtida diretamente da expressão exp:
summation(exp_expr.subs({x: 5}), [n, 0, oo]).evalf(), exp(5).evalf()E realmente é! Coerente. Mas e substituições vindas da série de Taylor?
Sabemos que a aproximação será tão melhor quanto mais termos houver na série. Vejamos isto, usando o valor anterior como referência:
print('n Taylor Diferença para exp(5)')
print('-'*45)
for i in range(0, 31, 5):
approx = series(exp(x), x, 0, i).removeO().subs({x: 5}).n()
approx = float(approx)
ref = float(exp(5).n())
print(f'{i:2} {approx:20} {approx-ref:15.4E}')n Taylor Diferença para exp(5) --------------------------------------------- 0 0.0 -1.4841E+02 5 65.375 -8.3038E+01 10 143.6894565696649 -4.7237E+00 15 148.37958007973663 -3.3579E-02 20 148.41310786833833 -5.1234E-05 25 148.41315907883663 -2.3740E-08 30 148.41315910257242 -4.1780E-12
Veja como realmente a diferença vai diminuindo. No entanto, será que dezenas de termos é razoável para ter uma diferença aceitável?
Aqui temos uma desvantagem da abordagem por séries de Taylor. Veja que estamos com séries construídas ao redor de x=0. No gráfico abaixo, vemos que mesmo ordens mais baixas fazem uma boa aproximação ao redor de tal valor. Porém, ao se afastar, como no caso de x=5, a aproximação só se torna aceitável com mais termos. E, caso ainda não tenha percebido, no caso da função exponencial não faz sentido fazer expansão ao redor de x=5 pois a derivada de uma exponencial é a própria exponencial. Ao redor de zero esse problema não existe. Por isso séries de Maclaurin são as que mais aparecem em exercícios, já que evitam problemas desse tipo. Voltaremos a discussões nesse sentido adiante.
from sympy.plotting import plot
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset
def move_sympy_plot_to_axes(sympy_plot, plt_ax):
"""Moves a SymPy plot to a Matplotlib axes
Adapted from: https://stackoverflow.com/a/46813804/8706250
Parameters
----------
sympy_plot : SymPy plot
plt_ax : Matplotlib axes
"""
backend = sympy_plot.backend(sympy_plot)
backend.ax = plt_ax
backend._process_series(backend.parent._series, plt_ax, backend.parent)
backend.ax.spines['right'].set_color('none')
backend.ax.spines['bottom'].set_position('zero')
backend.ax.spines['top'].set_color('none')
plt.close(backend.fig)
fig, ax = plt.subplots(figsize=(10, 6))
axins = zoomed_inset_axes(ax, 128, loc='upper center') # zoom = 128
p_exp = plot(exp(x), (x, -1, 6), show=False, label=r'$f(x) = exp(x)$')
move_sympy_plot_to_axes(p_exp, ax)
data_exp = p_exp[0].get_points()
# axins.plot(*data_exp)
points = []
points.append(data_exp)
for i in range(0, 31, 5):
taylor = series(exp(x), x, 0, i).removeO()
p_taylor = plot(taylor, (x, -1, 6), show=False, label=f"Taylor - ordem {i}")
move_sympy_plot_to_axes(p_taylor, ax)
data_taylor = p_taylor[0].get_points()
points.append(data_taylor)
# axins.plot(*data_taylor)
for p in points:
axins.plot(*p)
x1, y1 = 4.99, 148.0
x2, y2 = 5.005, 148.5
axins.set_xlim(x1, x2)
axins.set_ylim(y1, y2)
mark_inset(ax, axins, loc1=2, loc2=4, fc="none", ec="0.6")
ax.scatter(5, exp(5).n(), color='red', label='Ponto (5, exp(5))')
axins.scatter(5, exp(5).n(), color='red')
ax.legend()
ax.set_ylim(0, 150)
ax.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.show()Convergência de séries
Vimos anteriormente que durante muito tempo a ideia de que somas infinitas podem originar valores finitos era considerada paradoxal. E já demos muitos exemplos que mostram que é possível obter valores de algumas séries infinitas. Matematicamente, tais séries são convergentes. Daí o motivo do estudo de convergência de séries e os diversos critérios e testes de convergência vistos em disciplinas e livros de cálculo. Não cabe aqui ficar vendo tais testes porém, será que o SymPy é capaz de sinalizar se uma determinada soma converge?
Vamos criar um somatório a partir de uma expressão:
expr = (-1)**(x-1) / x
convergent01 = Sum(expr, (x, 1, oo))
convergent01O SymPy possui um método is_convergent que retorna um booleano:
convergent01.is_convergent()Ou seja, nesse exemplo temos um caso que converge. Mas para qual valor? Simples, basta usar o método doit para descobrir:
convergent01.doit()Vejamos um caso de divergência:
expr = 1/(2 * x)
divergent01 = Sum(expr, (x, 1, oo))
divergent01divergent01.is_convergent()divergent01.doit()Veja que o método is_convergent retornou False de forma que, ao solicitar que a soma fosse feita, o retorno foi infinito e não um valor específico. Coerente com uma série divergente.
Usualmente no estudo de séries convergentes aparecem as chamadas séries geométricas, com a seguinte definição:
from sympy import symbols
u, a = symbols('u a')
geom_series_expr = u**n * a
geom_series = Sum(geom_series_expr, (n, 0, oo))
geom_seriesVejamos o resultado do método doit:
geom_series.doit()Veja que há duas possibilidades, que dependem do valor de u. Vamos fazer substituições para ilustrar as duas possibilidades.
# u < 1, deve convergir:
geom_series.subs({a: 1, u: 1/2}).is_convergent()geom_series.subs({a: 1, u: 1/2}).doit()Assim, como u < 1, a série converge. No caso, para o valor 2.
Vendo um caso de divergência:
# u > 1, deve divergir
geom_series.subs({a: 1, u: 3/2}).is_convergent()geom_series.subs({a: 1, u: 3/2}).doit()A série diverge, daí a indicação de infinito no resultado.
Paridade de funções. Pêndulos
A paridade de funções é um conceito ligado à simetria. Funções pares ou ímpares podem simplificar muito algumas manipulações matemáticas visto que aparecem padrões em termos de séries. Para mais detalhes, veja este artigo sobre paridade de funções. Aqui, veremos como reconhecer se uma função é par ou ímpar a partir de sua série de Taylor. Aproveitaremos para discutir mais alguns aspectos dessas séries.
Vamos verificar a série de Taylor para a função seno ao redor de \theta=0:
from sympy import sin, cos, diff
theta = Symbol('theta')
series(sin(theta))As funções seno e cosseno podem ser relacionadas por suas derivadas. Já escrevemos sobre derivadas no SymPy:
diff(sin(theta), theta, 1), diff(cos(theta), theta, 1) # derivada primeira de cada funçãoLogo, nas séries de Taylor de ambas as funções deve haver alternância de seno e cosseno. Verifiquemos:
print(' Função seno')
print('n d^n(f(x))/dx d^n(f(x))/dx|x=0 Termo')
print('-'*45)
for i in range(8):
print(f'{i} {diff(sin(theta), theta, i)!s:^15} {diff(sin(theta), theta, i).subs(theta, 0)!s:^15} {sin(theta).taylor_term(i, theta)!s:^15}')Função seno n d^n(f(x))/dx d^n(f(x))/dx|x=0 Termo --------------------------------------------- 0 sin(theta) 0 0 1 cos(theta) 1 theta 2 -sin(theta) 0 0 3 -cos(theta) -1 -theta**3/6 4 sin(theta) 0 0 5 cos(theta) 1 theta**5/120 6 -sin(theta) 0 0 7 -cos(theta) -1 -theta**7/5040
Vemos que na série, expandida ao redor de zero, aparecem apenas termos com expoentes ímpares. Esta é uma característica de funções ímpares. Uma das diversas propriedades de tais funções é que f(-x) = -f(x).
Vejamos para a função cosseno:
series(cos(theta))print(' Função cosseno')
print('n d^n(f(x))/dx d^n(f(x))/dx|x=0 Termo')
print('-'*45)
for i in range(8):
print(f'{i} {diff(cos(theta), theta, i)!s:^15} {diff(cos(theta), theta, i).subs(theta, 0)!s:^15} {cos(theta).taylor_term(i, theta)!s:^15}')Função cosseno n d^n(f(x))/dx d^n(f(x))/dx|x=0 Termo --------------------------------------------- 0 cos(theta) 1 1 1 -sin(theta) 0 0 2 -cos(theta) -1 -theta**2/2 3 sin(theta) 0 0 4 cos(theta) 1 theta**4/24 5 -sin(theta) 0 0 6 -cos(theta) -1 -theta**6/720 7 sin(theta) 0 0
Vemos que na série aparecem apenas termos com expoentes pares. Esta é uma característica de funções pares. Uma das diversas propriedades de tais funções é que f(-x) = f(x).
Vamos aproveitar e mostrar graficamente como mais termos na série de Taylor aumentam a faixa de domínio na qual a aproximação é aceitável:
from sympy import pi
from matplotlib.ticker import FuncFormatter, MultipleLocator
fig, ax = plt.subplots(figsize=(10, 6))
p_sin = plot(sin(theta), (theta, -2*pi, 2*pi), show=False, label=r'$f(\theta) = sin(\theta)$')
move_sympy_plot_to_axes(p_sin, ax)
for i in range(0, 13, 2):
taylor = series(sin(theta), theta, 0, i).removeO()
p_taylor = plot(taylor, (theta, -2*pi, 2*pi), show=False, label=f"Taylor - ordem {i}")
move_sympy_plot_to_axes(p_taylor, ax)
ax.tick_params(axis='both', which='major')
def format_func(value, tick_number):
"""find number of multiples of pi/2"""
N = int(round(2 * value / pi.n()))
if N == 0:
return "0"
elif N == 1:
return r"$\dfrac{1}{2}\pi$"
elif N == 2:
return r"$\pi$"
elif N % 2 > 0:
return r"$\dfrac{{{0}}}{{2}}\pi$".format(N)
else:
return r"${0}\pi$".format(N // 2)
ax.xaxis.set_major_locator(plt.MultipleLocator(float(pi.n()) / 2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(float(pi.n()) / 4))
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
ax.set_xlabel(r'$\theta$')
ax.set_ylabel(r'$\sin(\theta)$')
ax.set_ylim(-3, 3)
ax.legend()
ax.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.show()A série foi construída ao redor de \theta=0. Desta forma, mesmo com poucos termos temos uma aproximação aceitável nas proximidades deste valor. No entanto, quanto mais distante deste valor, maior o erro com poucos termos. Mesmo com mais de 10 termos ainda não temos uma aproximação aceitável para os extremos do domínio apresentado na figura. É muito importante estar atento a esse fato.
Caso ainda esteja com dificuldade de associar o assunto com algo mais prático, vamos a um exemplo comum de aulas de física.
Provavelmente você estudou pêndulos em suas aulas de física do ensino médio:

Mas, no ensino médio, não deve ter visto a equação completa que representa o movimento do pêndulo com o tempo:
\frac{d^2 \theta}{dt^2} + \frac{g}{l} \sin(\theta) = 0Afinal, a beleza de equações diferenciais não é mostrada aos nossos jovens 🙁 Demonstração da equação neste link sobre pêndulos.
Na equação, g é a aceleração gravitacional; l é o comprimento do cabo do pêndulo; e \theta é o ângulo do cabo com a vertical.
O que deve ter sido apresentado a você é a variação de ângulo e o período são dados por:
\theta(t) = \theta_0 \cos \left( \sqrt{\frac{g}{l}}t \right) \\ T_0 = 2 \pi \sqrt{\frac{l}{g}}No entanto, caso tenha estudado equações diferenciais posteriormente, você vai perceber que tais fórmulas não são diretamente obtidas da equação diferencial. O que muitas vezes se omite do aluno, especialmente no ensino médio, é que as fórmulas só são válidas para ângulos muito pequenos, geralmente se considera \theta \ll 1 radiano. Ora, tal ângulo é bem próximo de zero e, portanto, podemos pegar poucos termos de nossa série de Taylor. Na realidade, podemos pegar apenas o primeiro termo:
\sin(\theta) \approx \theta \qquad \theta \ll 1Sendo essa condição válida, temos
\frac{d^2 \theta}{dt^2} + \frac{g}{l} \theta = 0Uma equação bem mais simples, de onde podem ser obtidas as fórmulas apresentadas anteriormente. Faça de exercício para praticar 🙂
Perceba como o trabalho de resolução fica muito mais simples com a aproximação oriunda da série de Taylor. Daí a importância de seu estudo.
Séries de Fourier. Transformadas de Fourier
Um artigo sobre séries não poderia deixar de fora as séries e transformadas de Fourier. As transformadas de Fourier são muito comuns em física e química, consistindo de uma manipulação matemática que reorganiza informação. Você pode imaginar, por exemplo, que o olho e o ouvido humanos realizam transformadas de Fourier analisando ondas eletromagnéticas e sonoras, respectivamente. O assunto é bem amplo e certamente aparecerá mais vezes aqui no site. Nosso objetivo aqui é abordar os principais aspectos e verificar como o SymPy realiza algumas manipulações básicas. Vamos começar com algumas definições.
Breve fundamentação matemática
Forma geral
A forma mais geral de uma série de Fourier é expressa como uma soma de funções seno e cosseno:
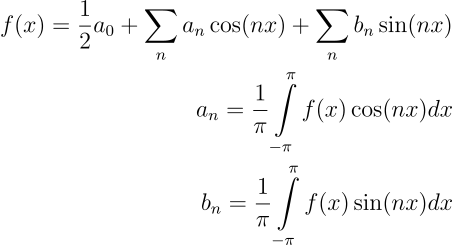
onde vemos que os coeficientes a_n e b_n derivam do comportamento ortonormal das funções seno e cosseno.
Séries de Fourier diferem das séries de Taylor em diversos aspectos. Aqui, cabe destacar dois:
- o intervalo de convergência é sempre entre -\pi e \pi nas séries de Fourier, enquanto que nas de Taylor, o intervalo muda de acordo com a função
- é raro encontrar funções que não possam ser expandidas em uma série de Fourier, enquanto que há mais exemplos de funções que não podem ser expandidas por Taylor
Mudando intervalo
Em alguns contextos, como em quântica, é útil mudar a faixa de um série de Fourier de (-\pi, \pi) para (-L, L). Para isso, a variável x deve ser substituída por \frac{\pi x}{L}:
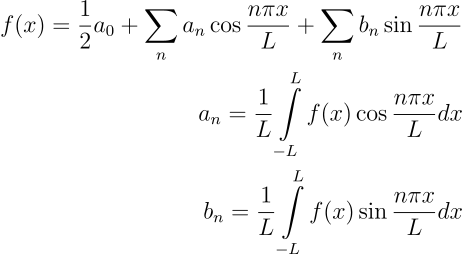
DFT
Já vimos aqui no site que as funções seno e cosseno se relacionam com a função exponencial através da fórmula de Euler. E já escrevemos sobre complexos também. Assim, podemos escrever outra forma para as séries de Fourier:
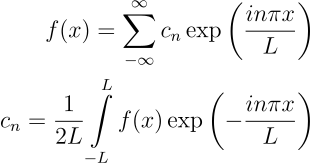
Neste caso, os coeficientes são complexos e a série representará apenas funções periódicas. No entanto, é possível modificar a equação para funções não periódicas. Considere k = \frac{n \pi}{L}. Agora, imagine L \to \infty. À medida em que L aumenta, mudanças em k ocorrem com incrementos menores a cada mudança em n. Ou seja, \Delta k = \frac{\pi}{L} \Delta n . No limite \Delta k \to 0, k se torna uma variável contínua, e os coeficientes c_k podem ser descritos como funções contínuas de k, c(k). Portanto, substituindo \Delta n = \frac{L}{\pi} \Delta k:
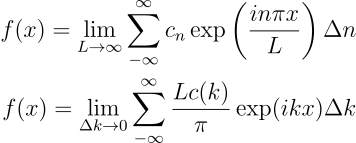
Ora, é a definição de uma integral. Fazendo \frac{Lc(k)}{\pi} = \frac{g(k)}{\sqrt{2\pi}}, temos:
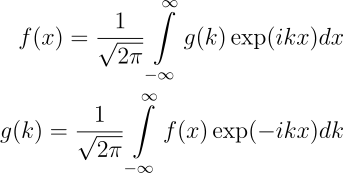
A equação de f(x) é chamada integral de Fourier, e f(x) e g(k) são chamadas transformadas contínuas de Fourier uma da outra. Para cálculos computacionais, por vezes é mais conveniente trabalhar com amostras discretas, o que dá origem às transformadas discretas de Fourier (DFT).
Por exemplo, suponha uma função do tempo, como seno ou cosseno, expressa como \sin(2\pi \nu t) ou \cos(2\pi \nu t). Como é uma função periódica, precisamos de amostras apenas para um período \tau_0. A função DFT é definida por
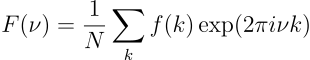
onde N é o número de amostras tomadas do período \tau_0 e k varia de -t a t-1 em inteiros centrados em zero. A transformada de Fourier é dita, então, que transforma a função do domínio do tempo para o domínio da frequência. Considerando a fórmula de Euler e^{i \theta} = \cos \theta + i \sin \theta:
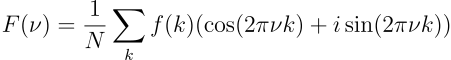
Obviamente, mais amostras levam a melhores saídas. Atualmente há o algoritmo transformada rápida de Fourier, que requer que o número de pontos seja uma potência de dois.
É conveniente separar a parte real da parte imaginária na equação anterior:
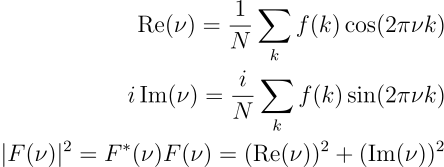
Onde |F(\nu)|^2 é o valor absoluto de F(\nu). Um gráfico de |F(\nu)|^2 versus \nu é chamado de espectro de potência da transformada de Fourier.
Diferença entre série de Fourier e transformada de Fourier
Veja na subseção anterior que a ideia de transformada de Fourier surgiu quando se buscou uma forma de obter séries para funções não periódicas. Esse é o ponto chave para a diferenciação.
Uma série de Fourier é usada para representar uma função periódica através de uma soma discreta de exponenciais complexas. Uma transformada de Fourier é usada para representar uma função geral, não periódica, através de uma contínua superposição ou integral de exponenciais complexas. Uma transformada de Fourier pode ser vista como o limite da série de Fourier de uma função quando o limite se aproxima do infinito, de forma que os limites de integração mudam de um período para (-\infty, \infty).
Paridade de funções
Por fim, vimos em Taylor que funções pares ou ímpares são convenientes por facilitar algumas manipulações matemáticas. O mesmo ocorre em séries de Fourier.
Para funções ímpares, os coeficientes a são nulos e a série se torna
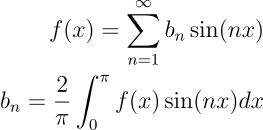
Para funções pares, os coeficientes b são nulos e a série se torna
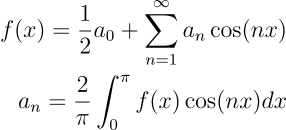
Essa foi uma muito breve revisão do tema. Certamente o assunto irá aparecer mais vezes aqui no site, então muitas aplicações serão vistas. Agora, vamos ver como o SymPy realiza operações de Fourier.
Séries de Fourier no SymPy
Podemos criar uma série de Fourier para uma função com fourier_series:
from sympy import fourier_series
fourier = fourier_series(f(x))
fourierObserve que foi fornecida na forma geral, deixando claro que é uma sequência de somas.
Podemos obter cada um dos coeficientes da forma geral:
fourier.a0fourier.anfourier.bnVimos na fundamentação matemática da seção anterior, que é comum representar o limite do intervalo por L. Podemos, então, verificar o limite do intervalo:
fourier.LTambém na seção anterior, vimos que podemos escrever na forma exponencial. Para isto, usamos o método rewrite solicitando que seja utilizada a função exp:
fourier.rewrite(exp)Vamos ver alguns exemplos mais práticos.
Gráficos e paridade de função
Vamos pegar como exemplo uma função bem simples: f(x) = x. Primeiro, vamos criar a série de Fourier para tal função:
from sympy import pi
s = fourier_series(x, (x, -pi, pi))
sQuanto à paridade, essa função é ímpar, afinal f(-x) = - f(x). Do que vimos anteriormente, os coeficientes a devem ser nulos:
s.a0, s.an, s.bnCom o método truncate podemos definir quantos termos queremos em nossa série. Por exemplo, com cinco termos:
s.truncate(5)O truncate, da forma utilizada acima, mostra apenas termos não nulos. Caso passemos None para o método, o mesmo retorna um gerador:
gen_fourier = s.truncate(None)
gen_fourier<generator object SeriesBase.__iter__ at 0x7f88dcbad4a0>
Podemos trabalhar com esse gerador com o islice, assim como fizemos anteriormente com séries de Taylor. Por exemplo, podemos gerar os 10 primeiros termos e armazenar numa tupla:
tuple(islice(gen_fourier, 10))Repare que o primeiro termo é zero, se referindo ao a_0 da forma geral de uma série de Fourier.
E qual o efeito do número de termos? No gráfico abaixo, vemos que quanto mais termos, melhor é a aproximação de nossa função:
fig, ax = plt.subplots(figsize=(10, 10))
axins = zoomed_inset_axes(ax, 2, loc='lower right') # zoom = 2
p_x = plot(x, (x, -3, 3), show=False, label=r'$f(x) = x$')
move_sympy_plot_to_axes(p_x, ax)
data_x = p_x[0].get_points()
axins.plot(*data_x)
for n in range(1, 16, 2):
fourier = s.truncate(n)
p_fourier = plot(fourier, (x, -3, 3), show=False, label=f"Fourier - n = {n}")
move_sympy_plot_to_axes(p_fourier, ax)
data_fourier = p_fourier[0].get_points()
axins.plot(*data_fourier)
x1, y1 = -0.5, -0.5
x2, y2 = 0.5, 0.5
axins.set_xlim(x1, x2)
axins.set_ylim(y1, y2)
mark_inset(ax, axins, loc1=1, loc2=2, fc="none", ec="0.6")
ax.legend()
plt.show()Caso ainda não tenha fica claro, veja na animação a seguir:
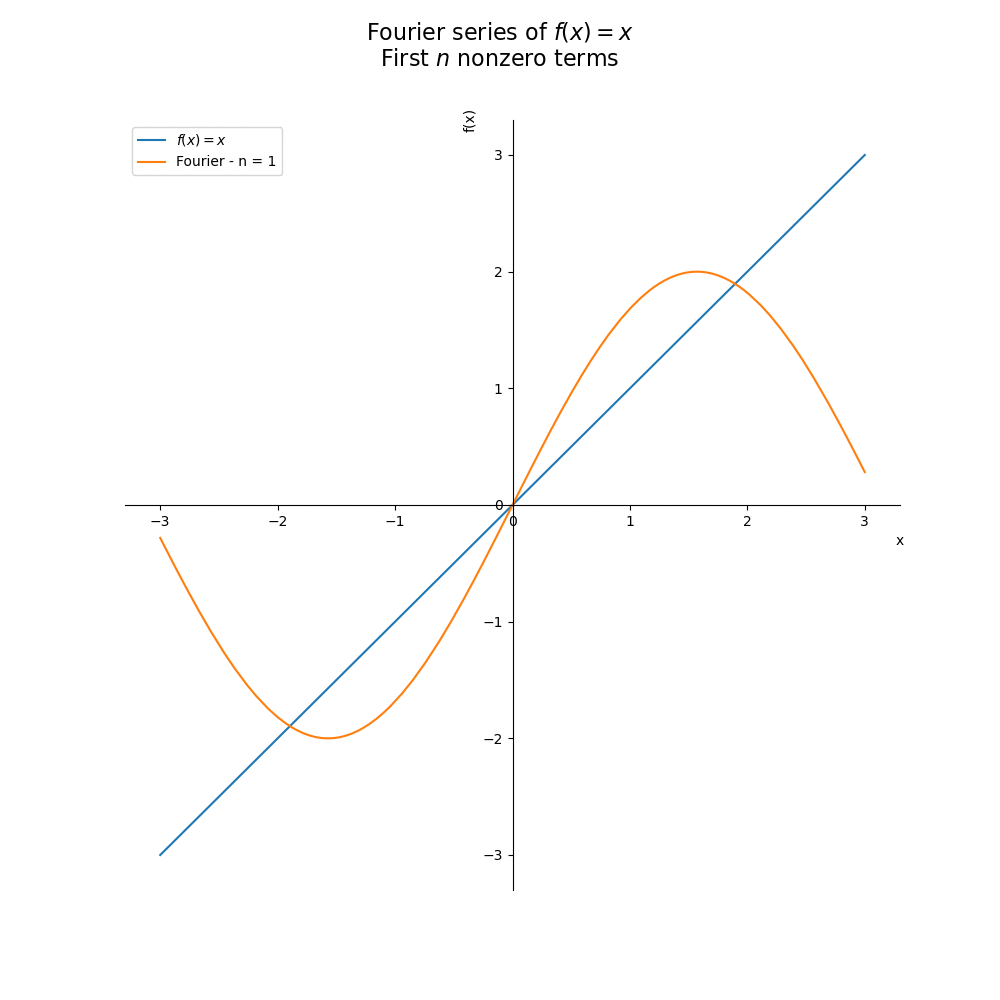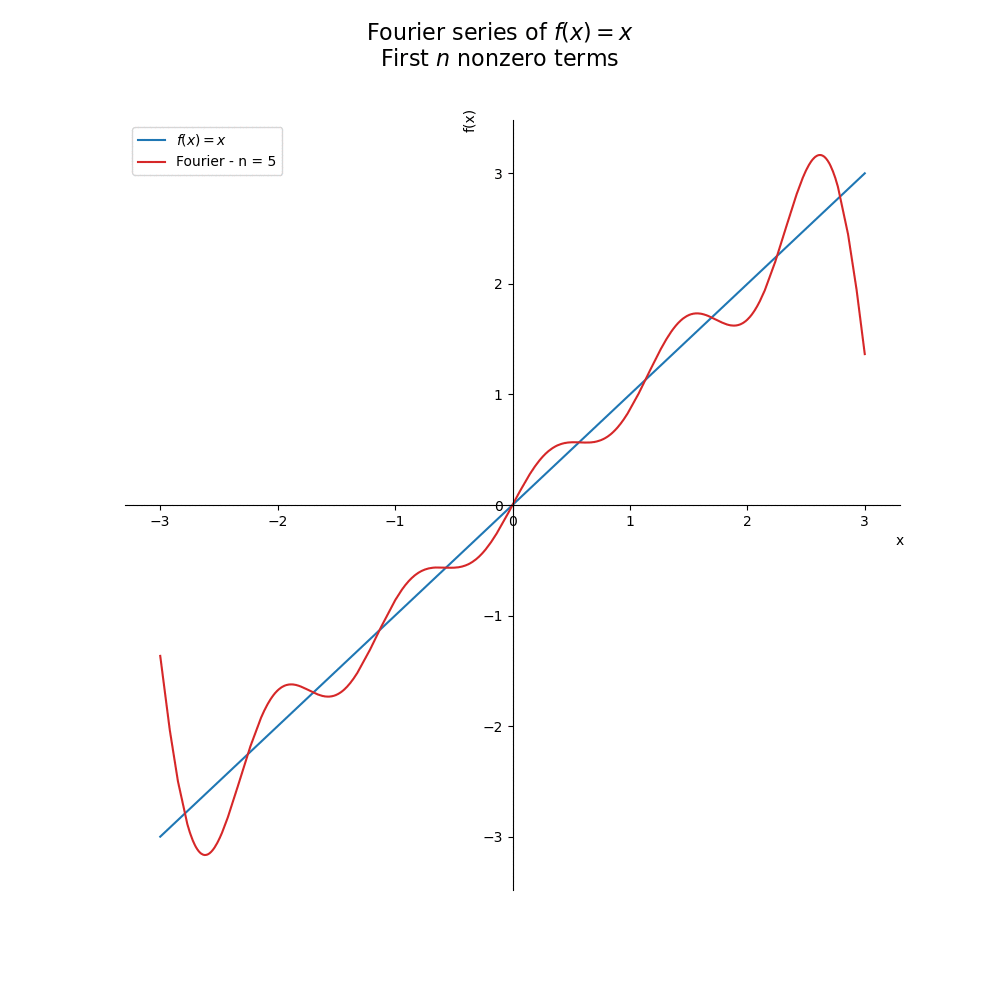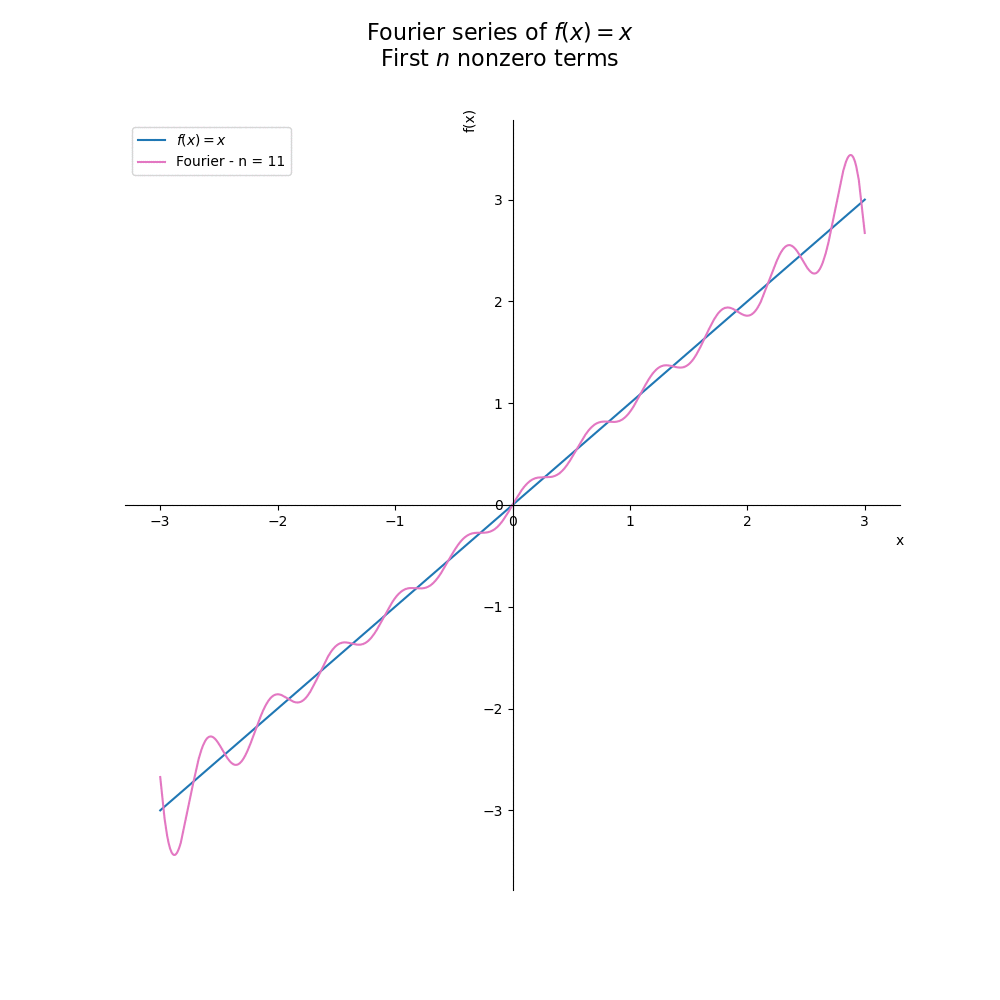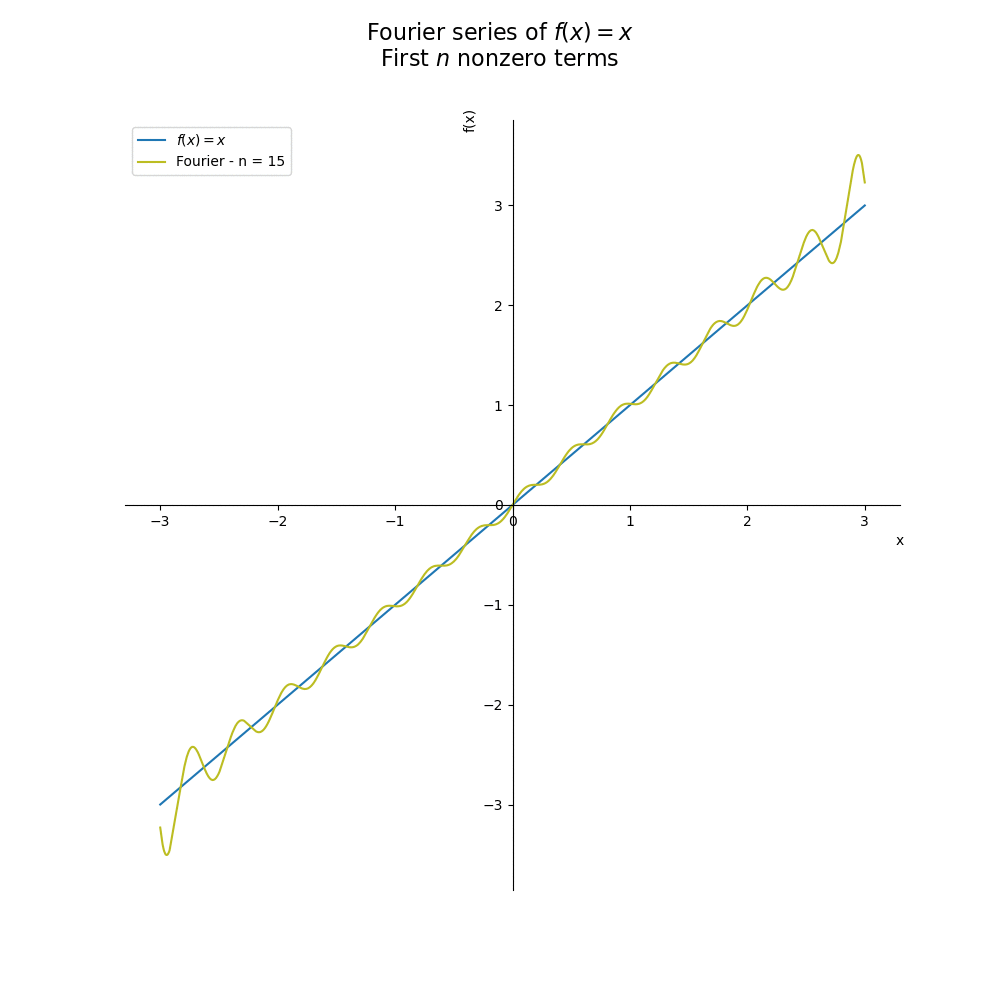
Aplicação em engenharia elétrica
Para deixar mais evidente a importância prática do assunto, vejamos uma aplicação real.
Um retificador é um dispositivo elétrico que converte corrente alternada em corrente contínua. Possuem diversas aplicações como, por exemplo, em fontes de alimentação para aparelhos eletrônicos. Vejamos um exemplo de um retificador de onda completa. Neste tipo de retificador, a onde de entrada é convertida em uma onda de polaridade constante (positiva ou negativa). Matematicamente, isso corresponde ao valor absoluto da função.
Vamos criar nossos símbolos e a expressão da função da onda de entrada:
from sympy import Abs
amplitude = Symbol('A', positive=True, real=True)
periodo = Symbol('P', positive=True, real=True)
x = Symbol('x', real=True)
expr_input = amplitude * sin((2 * pi / periodo) * x)
expr_inputVejamos o gráfico desta onda. Para exemplo, vamos considerar amplitude e período com valor 1:
from sympy.plotting import plot
plot(expr_input.subs({periodo: 1, amplitude: 1}), (x, -2, 2));Veja como é uma onda alternada. Como escrito anteriormente, o processo de retificação matematicamente equivale ao valor absoluto da função. Então, vamos obter a expressão utilizando a função Abs do SymPy:
expr_output = Abs(expr_input)
expr_outputPodemos fazer o gráfico desta nova função, com os mesmos valores de período e amplitude (que se referem à função de entrada):
plot(expr_output.subs({periodo: 1, amplitude: 1}), (x, -2, 2));Observe como no gráfico da onda retificada há apenas a parte positiva e o período foi dividido pela metade (passou de 1 para 0,5). Assim, a frequência de saída é o dobro da de entrada. Caso não tenha entendido, veja a figura de ambas as funções sobrepostas:
p_input = plot(expr_input.subs({periodo: 1, amplitude: 1}), (x, -2, 2), show=False, label='Input')
p_output = plot(expr_output.subs({periodo: 1, amplitude: 1}), (x, -2, 2), show=False, label='Output')
fig, ax = plt.subplots(figsize=(12, 6))
move_sympy_plot_to_axes(p_input, ax)
move_sympy_plot_to_axes(p_output, ax)
ax.lines[0].set(linestyle=':', linewidth=3)
ax.legend()
plt.show()Agora, vamos obter nossa série de Fourier (domínio da frequência) para a função da onda retificada (domínio do tempo):
s = fourier_series(expr_output, (x, 0, periodo))
sVamos explorar os coeficientes:
s.a0s.ans.bnVeja como os coeficientes b_n são nulos. Como vimos anteriormente, isto é característico de funções pares. O gráfico confirma que é uma função par, por ser simétrico com relação ao eixo y.
Vamos substituir valores na função. Apenas para exemplo, consideremos amplitude e período com valor 1, como feito anteriormente:
s.subs({periodo: 1, amplitude: 1}).anVeja como há alternância com termos nulos.
Agora, vamos ver o gráfico dessa série. Por ser uma série, precisamos definir quantos termos adicionaremos. Comecemos com um valor baixo, como 5:
plot(s.truncate(5).subs({periodo: 1, amplitude: 1}), (x, -2, 2));Veja que estranho. Nossa série até lembra a função, mas há uma parte negativa no gráfico. Vamos fazer o gráfico com mais termos. Por exemplo, com 10 termos:
plot(s.truncate(10).subs({periodo: 1, amplitude: 1}), (x, -2, 2));Agora temos uma melhor aproximação de nossa função. Se observar o gráfico, verá que os mínimos não estão encostando no eixo horizontal, o que seria esperado para os valores fornecidos. Se adicionarmos mais termos, teremos uma aproximação ainda melhor. Vejamos com 20 termos:
plot(s.truncate(20).subs({periodo: 1, amplitude: 1}), (x, -2, 2));Agora os mínimos estão mais próximos de zero. Poderíamos continuar colocando mais termos até que algum critério de aproximação fosse satisfeito.
Transformadas de Fourier no SymPy. Quântica
Para finalizar o assunto, vejamos a função fourier_transform. Vamos começar criando uma função:
expr = exp(-x**2)
exprA função criada é uma gaussiana bem simples. Funções gaussianas são muito estudadas pelas suas aplicações em estatística e em processamento de sinais. Vejamos seu gráfico:
plot(expr, (x, -5, 5));Agora, vamos fazer a transformada de Fourier utilizando a notação mostrada na parte teórica do artigo:
from sympy import fourier_transform
k = Symbol('k', real=True)
ft = fourier_transform(expr, x, k)
ftVeja que o uso da função fourier_transform é bem simples. A função que obtivemos de saída é, também, uma gaussiana. Aliás, essa é uma propriedade das gaussianas. Vamos ver o gráfico da função de saída da transformada:
plot(ft, (k, -5, 5));Observe que é uma gaussiana com largura menor que a gaussiana de entrada (antes da transformada). Vamos sobrepor os gráficos para deixar isto mais evidente:
p_input = plot(expr, (x, -5, 5), show=False, label='Input')
p_output = plot(ft, (k, -5, 5), show=False, label='Output')
fig, ax = plt.subplots(figsize=(12, 6))
move_sympy_plot_to_axes(p_input, ax)
move_sympy_plot_to_axes(p_output, ax)
ax.lines[0].set(linestyle=':', linewidth=3)
ax.set_xlabel('')
ax.set_ylabel('')
ax.legend()
plt.show()E esta é uma propriedade geral de funções e suas transformadas de Fourier: se uma função é mais “espalhada” em x, sua transformada de Fourier será mais “concentrada” em k. E vice-versa. Não é possível compactar arbitrariamente tanto a função quanto sua transformada. Esta é uma forma bem informal de enunciar um princípio de incerteza.
É bastante comum começar o estudo de transformadas de Fourier com sinais de áudio, daí a terminologia que já usamos neste artigo de dizer que a função de entrada é de domínio no tempo e a de saída, de domínio de frequência. Assim, em processamento de sinais, se diz que não é possível localizar precisamente um sinal (função de entrada) simultaneamente no domínio do tempo e no domínio de frequências (função de saída, transformada de Fourier).
Porém, nada impede que seja outro contexto. Por exemplo, em quântica as funções de onda momento e posição são pares de transformadas de Fourier dentro de uma margem de erro. Daí surge o famoso princípio da incerteza de Heisenberg. Não por acaso, aparecem diversas funções gaussianas durante o estudo de quântica. Aliás, gaussianas são muito comuns em diversos contextos.
Conclusão
Imaginou que seria possível em um mesmo texto sair de filosofia grega até quântica? E usando programação? Foi um artigo que me agregou muito enquanto escrevi e, espero, que agregue muito a você, leitor. Tão importante quanto saber como fazer operações matemáticas em alguma linguagem como Python, é saber o embasamento teórico para enxergar as diversas aplicações possíveis. E um pouco de história ajuda, não é mesmo? 🙂
Acompanhe o projeto Ciência Programada nas redes sociais para saber quando são publicados novos artigos, em breve escreverei mais sobre cálculo aplicado 😉
A lista completa de artigos sobre SymPy pode ser vista na categoria SymPy aqui do site.
Até a próxima.