Métodos de Monte Carlo são algoritmos computacionais que se baseiam em amostras aleatórias para obter resultados numéricos. Neste artigo, veremos como podemos obter o valor de pi com esses métodos.
Uma versão interativa do código mostrado nesta página, feita com Streamlit, pode ser utilizada online, clicando no botão a seguir:
Tópicos
Método de Monte Carlo
Métodos de Monte Carlo são algoritmos computacionais que se baseiam em amostras aleatórias para obter resultados numéricos. O princípio é utilizar aleatoriedade de dados para gerar resultados para problemas que, a priori, são determinísticos.
Um pouco de história
O nome Monte Carlo vem do fato de a ideia ter sido desenvolvida considerando jogos de azar, como de cassinos, pelo matemático Stanislaw Ulam. Assim, é uma referência ao Cassino de Monte Carlo, em Mônaco. Ulam buscava por métodos mais práticos para calcular a probabilidade de se obter boas mãos em jogos de carta. O leitor com conhecimentos de estatística e probabilidade deve estar pensando ser um problema já resolvido, pois se pode utilizar análise combinatória. No entanto, os cálculos podem ser laboriosos e demorados.

Ulam desenvolveu suas ideias em meados da década de 40. Naquele tempo, computadores estavam começando a ser desenvolvidos. Eram lentos, gigantes e pouco acessíveis. Agora é o momento de fornecer mais uma informação sobre Ulam: ele trabalhava no Laboratório Nacional de Los Alamos, onde se estudava armas nucleares no famoso Projeto Manhattan, que culminou no desenvolvimento das armas nucleares utilizadas na Segunda Guerra Mundial. Assim, pode ter acesso aos computadores mais potentes da época, como o ENIAC.

Ora, então porquê ele estava estudando jogos de cartas? Simples, ele estava doente e jogando muito enquanto se recuperava. Porém, logo percebeu que as ideias que estava desenvolvendo, poderiam ser aplicadas a problemas nucleares, como de difusão de nêutrons. Interessante, não?
Características
Os métodos variam, mas geralmente seguem os passos:
- Definir um domínio de possíveis inputs (entradas)
- Gerar inputs aleatoriamente a partir de uma distribuição de probabilidade sobre o domínio
- Realizar cálculos determinísticos sobre os inputs
- Agregar os resultados
São utilizados em diversos problemas científicos onde soluções analíticas são complexas ou impossíveis. Por exemplo, em modelos cinéticos de gases e dinâmica de fluidos. No entanto, há diversas aplicações em cenários mais abrangentes, como em análise de portfólios de ações no mercado financeiro.
Uma característica de tais métodos é utilizar um grande número de valores uniformemente distribuídos gerados aleatoriamente. Daí seu aumento de relevância com o aumento da capacidade computacional no decorrer dos anos, já que computadores mais potentes possuem maior capacidade de gerar números pseudo-aleatórios.
Do descrito até o momento, vemos que se trata de um estudo dentro da estatística inferencial, já que o objetivo é fazer afirmações a partir de um conjunto de valores representativo (amostra) sobre um universo. No caso, amostras aleatórias, que tendem a exibir as mesmas propriedades da população de onde são geradas.
Lei dos grandes números
No trecho anterior, foi citada a característica dos métodos de Monte Carlo utilizarem um grande número de valores aleatórios. Esta característica faz com que seja relevante no contexto a chamada lei dos grandes números. Tal lei é fundamental na teoria da probabilidade e descreve que a média aritmética dos resultados da realização da mesma experiência repetidas vezes tende a se aproximar do valor esperado à medida que mais tentativas se sucederem. Matematicamente,
Tal lei se tornará evidente nos exemplos a serem mostrados a seguir.
Cálculo do valor de pi
Recentemente, escrevemos aqui no site sobre o número pi, mostrando um pouco da história de como diferentes aproximações foram sendo utilizadas ao longo do tempo. Neste artigo, exploraremos outra maneira de se obter o valor, com um método de Monte Carlo.
O código Python utilizado aqui pode ser obtido clicando no botão a seguir, que o redirecionará para um repositório do GitHub:
O código pode ser baixado como um arquivo zipado ou o repositório pode ser clonado usando Git.
Uma versão interativa pode ser utilizada online, clicando no botão a seguir:
Tal versão interativa permite mudar os parâmetros (que serão detalhados a seguir) como mostra a seguinte animação:
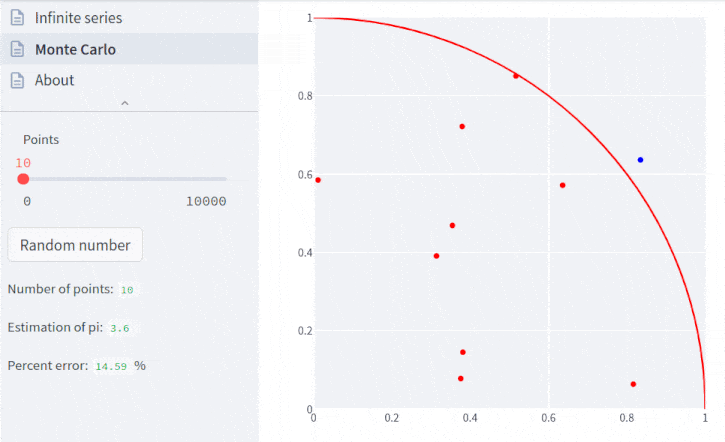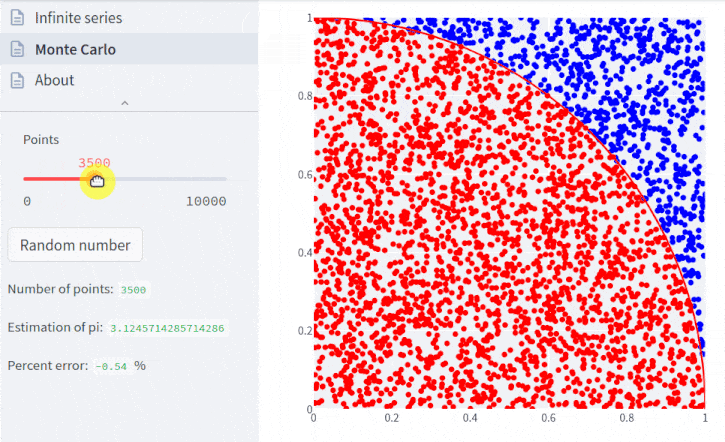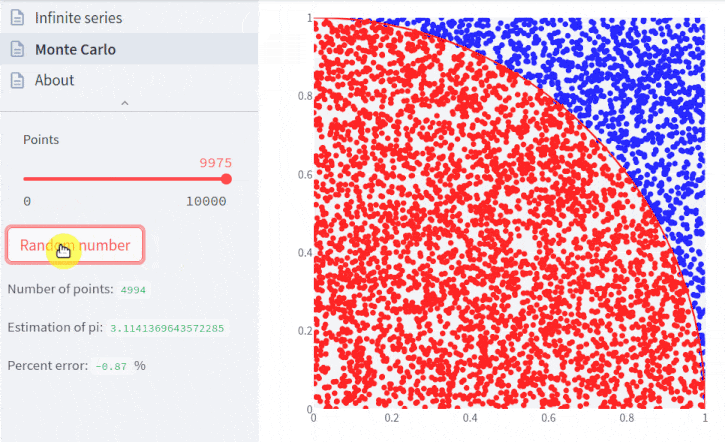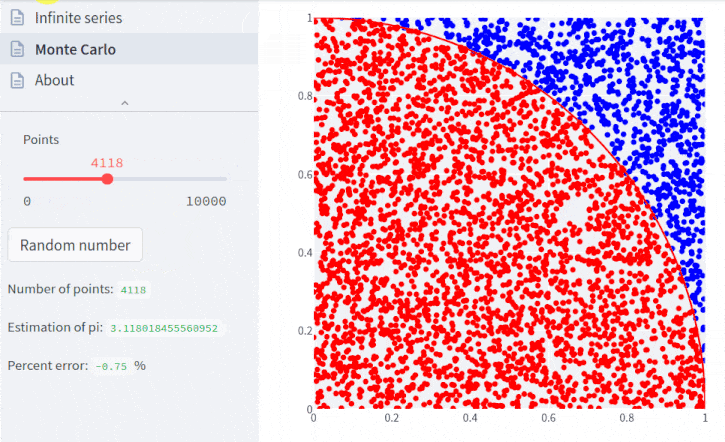
Para entender as etapas de cálculo, lembremos que a área de um quadrado é seu lado ao quadrado, e a área de um círculo é π vezes o raio ao quadrado.
Para calcular o valor de pi, vamos considerar os seguintes passos:
- desenhar um quadrado de lado unitário e inscrever um quadrante (setor circular correspondente a um quarto de circunferência) neste quadrado
- o raio da circunferência também será unitário
- a área do quadrado é a unidade e a área do quadrante é π / 4, de forma que a razão entre as áreas é π / 4
- distribuir uniformememnte um dado número de pontos neste quadrado
- contar o número de pontos que ficar dentro do setor circular
- a razão entre o número de pontos dentro do setor circular e o total de pontos é uma estimativa da razão entre as duas áreas, π / 4
- assim, para estimar o valor de pi, basta multiplicar a razão por 4
Imagino que esteja bem abstrato, então vamos visualizar. Na célula a seguir, importaremos o necessário para demonstrar o método com a linguagem Python. A classe PiMonteCarlo foi criada por mim e seu código está no repositório linkado anteriormente.
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import matplotlib.cm as cm
import matplotlib.ticker as mtick
import numpy as np
from src.compute_pi import PiMonteCarloVejamos os atributos e métodos desta classe. O papel de cada um será visto no decorrer do artigo.
[x for x in dir(PiMonteCarlo) if not x.startswith('_')]['calculate', 'coords', 'count_inside_quadrant', 'error', 'plot', 'points', 'seed']
A classe pode ser inicializada com um número inteiro, que representa o número de pontos a serem uniformemente distribuídos no quadrado de lado unitário. O método plot faz o gráfico do quadrado com os pontos:
pi = PiMonteCarlo(100)
pi.plot();Veja no gráfico acima que há pontos vermelhos e azuis. Os vermelhos representam os pontos que se encontram dentro de uma distância de 1 unidade para a origem do gráfico. Ou seja, os pontos que se encontram dentro do quadrante. Para facilitar, podemos utilizar o parâmetro booleano arc do método para desenhar o limite do quadrante:
pi.plot(arc=True);Na parte superior do gráfico aparece o número de pontos, o valor estimado para π e o erro da estimativa considerando o valor conhecido. No entanto, você deve estar com dificuldade de enxergar como os pontos se relacionam com um quadrante. Vamos aumentar o número de pontos:
pi.points = 1000
pi.plot();Agora, com 1000 pontos, deve estar mais fácil de visualizar o quadrante, mesmo com a ausência da linha auxiliar que o delimita. Vamos colocar a linha apenas para facilitar ainda mais:
pi.plot(arc=True);Cada ponto pode ser descrito por coordenadas, que podem ser visualizadas com a propriedade coords. Na célula seguinte, vemos as coordenadas dos 10 primeiros pontos:
pi.coords[:10](Coordinate(x=0.581428494323093, y=0.6131917506200556), Coordinate(x=0.5438194696485, y=0.4252612829893858), Coordinate(x=0.004676373123996713, y=0.8022562182039947), Coordinate(x=0.7927237972419394, y=0.31656658515605185), Coordinate(x=0.3573345769772017, y=0.8554767653880233), Coordinate(x=0.9126151772173419, y=0.8232838228460756), Coordinate(x=0.1376483536535691, y=0.0455611181699167), Coordinate(x=0.7713742399091441, y=0.24378362303324952), Coordinate(x=0.6374898695743463, y=0.491154209189236), Coordinate(x=0.18317750261662535, y=0.7442699731680038))
Agora, vamos entender o valor da estimativa apresentada acima do gráfico. Segundo as etapas de cálculo descritas anteriormente, precisamos contar quantos dos 1000 pontos se encontram dentro do raio do quadrante. O método count_inside_quadrant serve exatamente para isso:
pi.count_inside_quadrant()770
A próxima etapa, é dividir tal número pelo total de pontos e multiplicar por 4:
(pi.count_inside_quadrant() / len(pi.coords)) * 43.08
Assim, obtivemos exatamente o valor apresentado acima do gráfico. Mas, com o código da classe, não precisamos fazer a etapa manualmente. A propriedade calculate serve para isso:
pi.calculate3.08
Internamente, calculate faz exatamente a conta apresentada na célula anterior. Por fim, o método error calcula o erro da estimativa considerando o valor de pi conhecido atualmente:
pi.error()-0.01960555055392467
Veja que é o valor apresentado acima do gráfico, a única diferença é que o valor do gráfico é apresentado em porcentagem, sendo 100 vezes o valor da célula anterior.
Discutimos no início do artigo que as estimativas tendem a se tornar melhores quanto mais pontos forem utilizados. Perceba a palavra tendem, é uma tendência e não uma certeza, já que é um processo aleatório. Voltaremos a essa questão adiante. Primeiro, aumentemos o número de pontos para 10.000:
pi.points = 10_000
pi.plot();Veja que o quadrante é muito mais evidente agora. E o erro diminuiu, comparado ao valor do caso anterior.
E com 100.000 pontos:
pi.points = 100_000
pi.plot();Novamente, muito evidente o quadrante e menor erro.
Partindo para 1 milhão de pontos:
pi.points = 1_000_000
pi.plot();Veja como agora não há uma diferença significativa quando comparado ao caso anterior. Na parte inicial do artigo, vimos como há uma tendência a um valor à medida que o número de amostras aumenta. É isso que acabamos de testemunhar aumentando o número de pontos em cada exemplo.
Podemos formalizar um pouco melhor essa questão. Nas células a seguir, geramos 500 casos de exemplo, com número de pontos variando de 10 até 1 milhão. Ao final, geramos um gráfico mostrando a variação do erro percentual à medida que mais pontos são utilizados:
errors = []
points = []
for i in np.logspace(1, 6, 500):
points.append(int(i))
errors.append(PiMonteCarlo(int(i)).error())fig, ax = plt.subplots(figsize=(12, 6), facecolor=(1, 1, 1))
norm_colors = mcolors.SymLogNorm(linthresh=0.01, linscale=0.75,
vmin=np.min(errors), vmax=np.max(errors))
colormap = cm.seismic_r
ax.scatter(points, errors, c=errors, cmap=colormap, norm=norm_colors)
ax.semilogx()
ax.yaxis.set_major_locator(mtick.MultipleLocator(0.05))
ax.yaxis.set_major_formatter(mtick.PercentFormatter(1))
ax.grid(True, linestyle='dashed')
ax.set_axisbelow(True)
ax.set_title('Change in error as the number of points increases',
size=18)
scalarmappable = cm.ScalarMappable(norm=norm_colors, cmap=colormap)
scalarmappable.set_array(errors)
colorbar = fig.colorbar(scalarmappable,
format=mtick.FuncFormatter(lambda x, pos: "{:.2%}".format(x)),
ticks=mtick.FixedLocator([-0.25, -0.1, -0.05, -0.01, -0.005,
0, 0.005, 0.01, 0.05, 0.1, 0.25]))
plt.show()Veja que o gráfico apresenta simetria, mostrando que os erros podem ser positivos ou negativos e tendem a ocorrer de forma aleatória. Veja que, mesmo com poucos pontos, pode acontecer de haver simulações com erros baixos (pontos com coloração mais fraca). No entanto, isso se torna cada vez mais comum com mais pontos, indicando que o valor estimado se aproxima cada vez mais do real. A partir de 10.000 pontos praticamente todas as estimativas já se encontram abaixo de 1 % de erro.
Por fim, ainda há um atributo da classe que não foi discutido, o seed. Para ficar mais evidente seu papel, vamos redefinir o número de pontos para um valor relativamente baixo, como 50:
pi.points = 50
pi.plot();O que acontece se passarmos novamente o número de pontos como 50:
pi.points = 50
pi.plot();Veja que, mesmo que o número de pontos solicitado seja o mesmo, o posicionamento dos mesmos mudou, assim como a estimativa do valor de pi. Isto ocorre pois, internamente, a classe utiliza um gerador aleatório. Mais especificamente, o gerador aleatório do NumPy. Assim, mesmo que o número de pontos solicitado seja o mesmo, não necessariamente terão as mesmas coordenadas.
No entanto, usualmente quando falamos de números aleatórios produzidos por programas estamos, na realidade, falando de números pseudo-aleatórios. Ou seja, números que parecem aleatórios mas são obtidos por algoritmos. Tais algoritmos costumam partir do que chamamos de seed (“semente”). Desta forma, se inicializarmos um gerador de números pseudo-aleatórios com uma mesma seed, os resultados obtidos serão sempre os mesmos.
Quando iniciamos a nossa classe, não fornecemos um valor de seed. Assim, esse valor será alterado sempre. No entanto, podemos fixar este valor:
pi.seed = 42
pi.points = 50
pi.plot();Agora, vamos novamente solicitar 50 pontos, duas vezes seguidas:
pi.points = 50
pi.plot();pi.points = 50
pi.plot();Observe que foram apresentados os mesmos pontos (mesmas posições nos gráficos) e as mesmas estimativas. Se mudarmos a seed ou reiniciarmos, passando None, as coordenadas mudarão:
pi.seed = 0
pi.points = 50
pi.plot();O assunto números aleatórios (ou pseudo-aleatórios) é bem extenso e será coberto em outro artigo em um futuro breve. Mas fica de conhecimento que, em computação, nem tudo que parece aleatório realmente é. Os links apresentados, em especial o da documentação do NumPy, são grandes fontes de informação a respeito.
Recomendações de leitura
O número pi é estudado há séculos, desde os tempos antigos, como já abordei em outro artigo. Por exemplo, Arquimedes fez estimativas utilizando geometria. Para mais detalhes do trabalho de Arquimedes, recomendo o livro Arquimedes: uma porta para a ciência de Jeanne Bendick, da incrível Coleção Imortais da Ciência. Clique nos links ou na imagem a seguir para mais detalhes.
Para matemática em geral, há O livro da matemática, da coleção As grandes ideias de todos os tempos. Clique nos links ou na imagem a seguir para mais detalhes.
Quem quiser se aprofundar em métodos de Monte Carlo, pode comprar o livro Monte Carlo Statistical Methods. Clique nos links ou na imagem a seguir para mais detalhes.
Por fim, um bom livro para iniciantes em Python é o Automatize tarefas maçantes com Python. Um livro com exemplos práticos e de fácil leitura. Clique nos links ou na imagem a seguir para mais detalhes.
Conclusão
Os métodos de Monte Carlo são muito importantes dentro do contexto científico. Neste artigo, utilizamos recursos visuais para compreender a natureza de tais métodos.
Já vimos em outro artigo que há métodos bem rápidos e exatos para obter o número pi, de forma que o método apresentado aqui na prática não é utilizado para estimar pi quando grande exatidão é necessária. No entanto, em outras áreas da ciência acaba sendo uma das melhores alternativas disponíveis para estimativas de quantidades, especialmente com o poder computacional cada vez mais disponível atualmente. A visualização apresentada aqui é didática e serve de referência para outras aproximações em outros contextos.
Acompanhe o projeto Ciência Programada nas redes sociais para saber quando são publicados novos artigos, em breve escreverei mais sobre Monte Carlo 😉
Até a próxima.











Bom dia. adoro o seu trabalho. Eu tive a oportunidade de participar do PyMat e assistir a sua apresentação sobre o uso do Streamlit no ensino educacional. Atualmente sou aluno do curso de matemática e quero aprender cada vez mais sobre as novas tecnologias que possamos usar, seja na educação ou no mercado de trabalho. Se estiver interessado gostaria de conversar contigo.
Bom dia, Gabriel. Claro, se tiver LinkedIn, me mande mensagem privada por lá que costumo olhar com mais frequência. Abraço