Aprendemos em matemática que só podemos somar matrizes de mesma ordem. E tal soma resulta em uma matriz de mesma ordem daquelas que foram somadas. A multiplicação de matrizes também possui uma exigência, a de que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz. Mas, em problemas matemáticos computacionais, por vezes temos matrizes ou vetores de diferentes ordens que gostaríamos de somar ou multiplicar que não cumprem as exigências citadas. Veremos neste artigo como o conceito de broadcasting do NumPy é útil nestes contextos e como ele se relaciona com quantização vetorial.
Tópicos
Definições matemáticas
Apenas para se certificar que todos estão com a mesma base, vamos colocar rapidamente as definições matemáticas para a adição e a multiplicação de matrizes, com um exemplo de cada operação.
Para somar duas matrizes, estas devem ter o mesmo número de linhas e de colunas e o resultado terá estes mesmos números de linhas e colunas. Matematicamente, a operação de soma entre uma matriz A e uma matriz B resultando em uma matriz C pode ser descrita como:
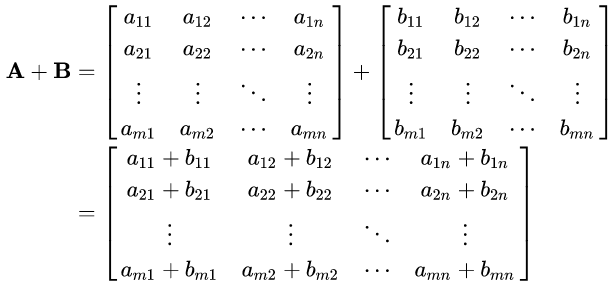
Resumidamente, cada item da matriz C pode ser descrito como:
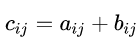
Como exemplo, veja a seguinte soma:
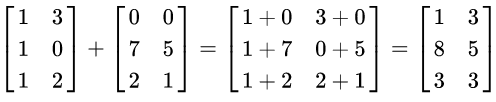
Para multiplicação, o número de colunas da primeira matriz deve ser igual ao número de linhas de segunda matriz. A matriz resultante tem o número de linhas da primeira e o número de colunas da segunda matriz. Em notação matemática, temos:
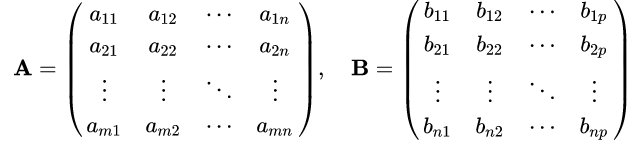
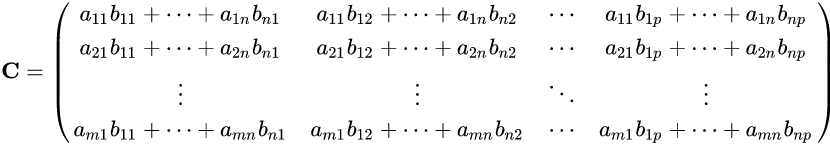
Ou, de forma mais sucinta, cada item da matriz C pode ser descrito como:
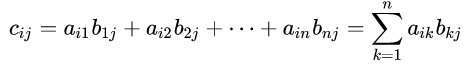
com i variando de 1 até m, e j indo de 1 até p, considerando que A é uma matriz m x n e que B é uma matriz n x p.
Eis um exemplo:
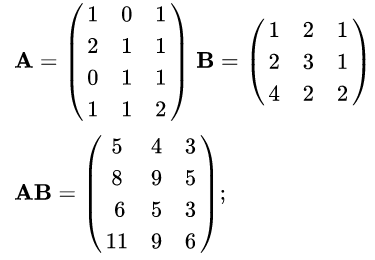
A notação matemática e os exemplos foram retirados da Wikipedia.
Agora que relembramos as definições, vamos ao Python.
Arrays em Python puro?
Se você clicou neste artigo, é muito provável que já esteja levemente familiarizado com o NumPy para cálculos numéricos. Talvez já seja até natural começar importando a biblioteca sem nem pensar muito no início de qualquer problema numérico. Mas, vamos dar um passo para trás e pensar nos motivos que fazem o com que NumPy seja a biblioteca mais usada para cálculos computacionais com Python.
Em um primeiro momento, poderíamos considerar utilizar listas. Afinal, poderíamos colocar nossos dados numéricos e, por exemplo, solicitar uma soma como mostrado a seguir:
a = [1, 2, 3]
b = [1, 2, 3]
c = a + b
c[1, 2, 3, 1, 2, 3]
Já vemos que o resultado não é o esperado matematicamente. O que ocorre é a concatenação das listas e não a soma item a item. Tente fazer a multiplicação e verá que nem ao menos está definida entre listas. Teste com tuplas também e não terá o resultado desejado.
Há ainda outro motivo para não utilizar as listas nativas do Python. Elas aceitam diversos tipos como itens de uma mesma lista. Por exemplo:
["a", 1, [True, False], 2.0]['a', 1, [True, False], 2.0]
Imagine fazer operações numéricas, ou mesmo não numéricas, com uma lista como essa. Não faria sentido. Daí o Python lidar com listas como um armazenamento mutável de itens que podem ser de tipos distintos. O símbolo “+” na primeira célula de código deste artigo, no contexto de listas, apenas simboliza para o interpretador Python que as duas listas devem ser unidas numa única, não fazendo qualquer diferença os tipos de seus itens. No entanto, seria interessante ter algum objeto que pudesse restringir o tipo de item que pode conter.
Daí haver o conceito de arrays em programação. Array é mais um de diversos termos em inglês que costumam ser utilizados em textos mesmo quando estes não são escritos em inglês. E este artigo não será diferente. Mas é importante termos uma ideia clara de seu significado e, considerando que está lendo este texto, é de se supor que você entenda português. Logo, é natural que busque por traduções do termo para português para facilitar sua compreensão.
Uma tradução por vezes utilizada para array é vetor. Considerando um contexto de operações matemáticas, é uma tradução aceitável e aqui mesmo no site já foi utilizada em alguns artigos. Mas é importante saber que há uma tradução mais geral e válida para qualquer contexto. Perceba que introduzi o termo quando estava mostrando o problema de listas aceitarem diversos tipos em sua sequência itens. Assim, as melhores traduções de array seriam ou arranjo, ou sequência. E, no contexto de programação, uma sequência de itens de mesmo tipo. Esta última parte é a mais importante. Para uma boa discussão sobre tradução deste e de outros termos recomendo este link.
Saber que todos os itens de array são de um mesmo tipo é o que garante previsibilidade em operações. Além de conseguirmos ter um melhor gerenciamento de memória, mas não entraremos neste último aspecto aqui.
Bom, agora que sabemos do que estamos falando, vejamos se há implementações nativas em Python para arrays.
Na instalação padrão do Python, há o módulo array de onde podemos importar o construtor array. Como já ressaltado, os itens de um array devem ser do mesmo tipo. Neste módulo, a forma de indicar o tipo é através de um código de tipo, uma letra colocada antes da passagem dos itens que indica o tipo esperado. Por exemplo, passando a letra u indicamos que se trata de um array de caracteres unicode:
import array
a = array.array("u", ["a", "b", "c"])
a array('u', 'abc')
Seguindo a lógica, a letra i indica que o array é de inteiros:
a = array.array("i", [1, 10, 20])
a array('i', [1, 10, 20])
Todos códigos de tipos são listados na documentação.
Se tentarmos passar um item que não é do tipo indicado, um TypeError é apresentado:
# observe como misturar o float 1.0 com os inteiros 10 e 20 resulta em erro
try:
a = array.array("i", [1.0, 10, 20])
except TypeError as e:
print(repr(e)) TypeError('integer argument expected, got float')
Agora, nosso objetivo aqui é fazer operações matemáticas. Será que o módulo lida com isso naturalmente?
a = array.array("i", [1, 2, 3])
b = array.array("i", [1, 2, 3])
c = a + b
c array('i', [1, 2, 3, 1, 2, 3])
Não… como vemos, o objeto array nativo do Python lida com o problema de diferentes tipos. Mas não é adequado para operações matemáticas com arrays numéricos. Daí a necessidade de usar uma biblioteca externa, sendo o NumPy a mais utilizada.
Arrays com NumPy. Broadcasting.
Bom, vamos logo ver que o NumPy realiza corretamente a operação matemática que estamos utilizando de exemplo:
from numpy import array
a = array([1, 2, 3])
b = array([1, 2, 3])
c = a + b
c array([2, 4, 6])
O resultado é o esperado considerando a definição matemática que vimos no início do artigo. Agora, considere a célula a seguir:
a = array((1, 2, 3))
b = 2
c = a + b
carray([3, 4, 5])
O resultado é intuitivo, concorda? O que o NumPy faz é, virtualmente, replicar o valor 2 em um array de três itens iguais e realizar a soma. Atenção ao virtualmente. Não é que o NumPy crie efetivamente cópias em memória, isto seria ineficiente, é apenas uma analogia para facilitar a compreensão. Veja a figura a seguir para compreender melhor o que foi escrito:
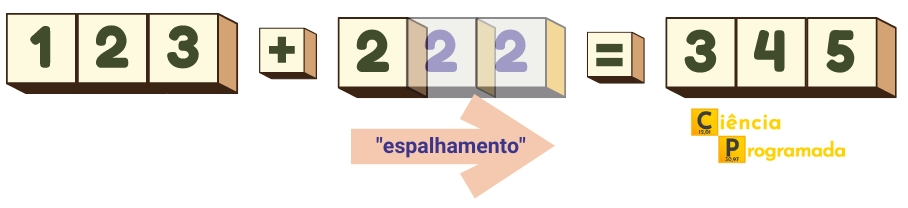
Esta replicação é chamada de broadcasting que, em uma tradução bem literal, seria “lançamento espalhado”. A tradução faz sentido tendo em vista que há o “espalhamento” de valores até que a dimensão desejada seja alcançada. Cabe lembrar que a transmissão de mensagens para receptores espalhados em telecomunicações usa o mesmo termo. Por exemplo, a famosa emissora, ou transmissora se preferir, BBC tem sua sigla originada de British Broadcasting Corporation. Há interessantes discussões sobre o termo broadcasting em programação neste link do StackOverflow e sobre a tradução do termo no StackExchange da língua portuguesa.
Agora vamos começar a aprofundar nossa discussão. Podemos descrever a operação acima como a soma de um escalar, o número 2, à uma matriz unidimensional.
Recentemente, no artigo sobre reshape do NumPy, fizemos algumas discussões sobre dimensões de arrays do NumPy. O atributo ndim mostra que nosso array a tem dimensão 1:
a.ndim1
Um comportamento análogo se observa com uma matriz bidimensional:
A = array([[1, 2, 3], [1, 2, 3]])
Aarray([[1, 2, 3],
[1, 2, 3]])
A.ndim2
C = A + b
Carray([[3, 4, 5],
[3, 4, 5]])
Veja como o comportamento de (virtual) replicação do escalar para efetuar a soma se repetiu.
Podemos verificar o que ocorre na soma entre um array bidimensional e um unidimensional:
A = array([[1, 2, 3], [1, 2, 3]])
b = array([1, 2, 3])
C = A + b
Carray([[2, 4, 6],
[2, 4, 6]])
Novamente, percebemos que o array b teve sua linha “replicada” para baixo de forma a permitir a soma.
Limitações do broadcasting
Não restam dúvidas que o broadcasting do NumPy agiliza muito operações numéricas. No entanto, não é sempre que é possível para a biblioteca efetuar tal procedimento. Há regras que definem quando é possível haver broadcasting. Considere dois arrays, o NumPy irá comparar seus elementos começando pela dimensão mais à direita. As dimensões são compatíveis quando seus tamanhos:
- são iguais, ou
- uma delas tem tamanho 1
Se essas condições não forem observadas, será dada a exceção ValueError: operands could not be broadcast together.
Os arrays de início não precisam ter o mesmo número de dimensões. E o array resultante terá o mesmo número de dimensões do array inicial com mais dimensões, onde o tamanho de cada dimensão é o maior tamanho da dimensão correspondente entre os arrays iniciais. Dimensões ausentes são consideradas de tamanho um.
Certamente os parágrafos anteriores foram bem abstratos, então vamos para um exemplo. Considere novamente A, b e C definidos como o último exemplo e seus respectivos dimensão, shape e tamanho:
from numpy import array2string
A = array([[1, 2, 3], [1, 2, 3]])
b = array([1, 2, 3])
C = A + b
def tabela_broadcasting(names, arrays, alignment=(5, 4, 6, 4)):
columns = ("array", "ndim", "shape", "size")
print(" | ".join([f"{col:^{align}}" for col, align in zip(columns, alignment)]))
print(" | ".join([f"{'-'*align}" for align in alignment]))
for name, arr in zip(names, arrays):
elements = (name, arr.ndim, arr.shape, arr.size)
print(
" | ".join(
[f"{str(el):^{align}}" for el, align in zip(elements, alignment)]
)
)
print("C =", array2string(C, prefix="C = "))
print()
tabela_broadcasting(("A", "b", "C"), (A, b, C)) C = [[2 4 6]
[2 4 6]]
array | ndim | shape | size
----- | ---- | ------ | ----
A | 2 | (2, 3) | 6
b | 1 | (3,) | 3
C | 2 | (2, 3) | 6
Caso tenha dificuldade em entender o que são ndim, shape e size, veja este artigo aqui do site.
Vamos entender as regras por partes considerando o resultado acima:
- os arrays iniciais são A e b
- as dimensões são 2 e 1, respectivamente
- a dimensão mais à direita de ambos tem tamanho 3, sendo iguais, permitindo broadcasting
- a próxima dimensão, seguindo para a esquerda, em A é 2 e em b é 1 (por ausência), permitindo broadcasting
- o array resultante C tem dimensão 2 (maior entre A e b), com tamanhos (2, 3), igual ao array A (maior dentre os iniciais)
O exemplo de um array somado com um escalar pode ser melhor entendido com base nas regras vistas:
a = array((1, 2, 3))
b = 2
c = a + b
print("c =", array2string(c, prefix="c = "))
print()
tabela_broadcasting(("a", "b", "c"), (a, array((b,)), c)) c = [3 4 5] array | ndim | shape | size ----- | ---- | ------ | ---- a | 1 | (3,) | 3 b | 1 | (1,) | 1 c | 1 | (3,) | 3
Comparando com as regras:
- os arrays iniciais são a e b
- as dimensões são 1 e 1, respectivamente
- a dimensão mais à direita de a tem tamanho 3, e de b tem tamanho 1, permitindo broadcasting
- o array resultante c tem dimensão 1 (maior entre a e b), com tamanho 3, igual ao array a (maior dentre os iniciais)
Consideremos um exemplo onde o broadcasting não é possível. Abaixo, redefinimos nossos arrays e tentamos realizar a soma:
A = array([
[1, 2, 3],
[1, 2, 3]])
b = array([1, 2])
try:
C = A + b
except ValueError as e:
print(repr(e))ValueError('operands could not be broadcast together with shapes (2,3) (2,) ')
Veja que a soma não foi possível, dando um erro que cita o shape dos arrays. Os tamanhos das dimensões mais a direita de cada array são distintos entre si e nenhum tem valor 1 logo, não é possível a operação. Compare cada atributo dos arrays na tabela a seguir:
tabela_broadcasting(("A", "b"), (A, b)) array | ndim | shape | size ----- | ---- | ------ | ---- A | 2 | (2, 3) | 6 b | 1 | (2,) | 2
Aplicação: quantização vetorial
Este conceito aparentemente simples de broadcasting está no cerne de uma das aplicações mais importantes em tecnologia da informação: quantização vetorial.
O que é quantização?
Quantização é o processo de restringir um conjunto contínuo ou grande de valores (tais como números reais) a um conjunto discreto (como números inteiros). Por exemplo:
| Entrada | Quantização |
|---|---|
| 0 < x ≤ 1 | 0,5 |
| 1 < x ≤ 2 | 1,5 |
| 2 < x ≤ 3 | 2,5 |
No caso acima, temos conjuntos infinitos de números reais em cada intervalo restringidos a um valor único, o centro de cada intervalo. Estes valores únicos são chamados de símbolos de quantização. Considerando que podemos expandir a tabela acima indefinidamente seguindo a lógica, se tivermos uma entrada como 5,8 esperamos como saída 5,5.
O exemplo acima é de quantização escalar, já que as entradas se tornam um número único que representa a amostra.
Vamos criar uma função que realize quantizações escalares, com auxílio do método digitize do NumPy. O digitize retorna um array de índices que indicam em qual intervalo cada valor de entrada se encontra. Podemos usar esses índices para obter os símbolos de quantização correspondentes aos itens do array de entrada:
from numpy import digitize, linspace, printoptions
def scalar_quantization(input_array, cut_points, quantization_symbols):
"""
Realiza quantização escalar
"""
# Encontrando os índices dos intervalos correspondentes a cada valor de entrada
quantized_indexes = digitize(input_array, cut_points, right=True) - 1
# Usando os índices para obter os símbolos de quantização correspondentes
quantized_array = quantization_symbols[quantized_indexes]
return quantized_array
# ---------- Primeiro exemplo:
# Definindo os pontos de corte dos intervalos
cut_points_first_example = [0, 1, 2, 3]
# Definindo os símbolos de quantização para cada intervalo
quantization_symbols_first_example = array([0.5, 1.5, 2.5])
# Gerando um array de valores de entrada
first_example = linspace(0.001, 3, 10)
# Imprimindo os resultados
print("Primeiro exemplo")
with printoptions(precision=3, suppress=True):
print("Valores de entrada:\n", first_example)
print(
"Valores de saída após a quantização:\n",
scalar_quantization(
first_example, cut_points_first_example, quantization_symbols_first_example
),
)Primeiro exemplo Valores de entrada: [0.001 0.334 0.667 1.001 1.334 1.667 2. 2.334 2.667 3. ] Valores de saída após a quantização: [0.5 0.5 0.5 1.5 1.5 1.5 2.5 2.5 2.5 2.5]
Considere agora a tabela a seguir:
| Entrada | Quantização |
|---|---|
| -0.5 < x ≤ 0,5 | 0 |
| 0.5 < x ≤ 1,5 | 1 |
| 1.5 < x ≤ 2,5 | 2 |
Neste último caso, ainda temos que a quantização restringe o intervalo para o valor central. E, seguindo a lógica, se tivermos uma entrada como 5,8 esperamos como saída o valor 6. Podemos aplicar nossa função a esse segundo exemplo:
# ---------- Segundo exemplo:
# Definindo os pontos de corte dos intervalos
cut_points_second_example = [-0.5, 0.5, 1.5, 2.5]
# Definindo os símbolos de quantização para cada intervalo
quantization_symbols_second_example = array([0, 1, 2])
# Gerando um array de valores de entrada
second_example = linspace(-0.499, 2.5, 10)
# Imprimindo os resultados
print("Segundo exemplo")
with printoptions(precision=3, suppress=True):
print("Valores de entrada:\n", second_example)
print(
"Valores de saída após a quantização:\n",
scalar_quantization(
second_example, cut_points_second_example, quantization_symbols_second_example
),
)Segundo exemplo Valores de entrada: [-0.499 -0.166 0.167 0.501 0.834 1.167 1.5 1.834 2.167 2.5 ] Valores de saída após a quantização: [0 0 0 1 1 1 2 2 2 2]
Observe nos dois exemplos que estamos pegando uma entrada de valores e simplificando-os em uma saída, que possui limites, restrições. Podemos pensar como se os dados de entrada estivessem sendo comprimidos em um formato em particular. É exatamente essa a principal aplicação do conceito: compressão de dados. E não precisamos ficar restrito à apenas uma dimensão, daí a aplicação do conceito de vetores.
Quantização vetorial
A quantização vetorial é uma técnica de compressão de dados amplamente utilizada em processamento de imagens e sinais. Ela é baseada na ideia de agrupar vetores de dados em clusters e, em seguida, substituir cada vetor pelo centroide do cluster mais próximo. Isso reduz a quantidade de dados que precisam ser armazenados ou transmitidos, sem afetar muito a qualidade da informação.
Em outras palavras, a quantização vetorial é uma técnica de redução de dados, onde a informação é mapeada para um número menor de símbolos. Ela é útil em situações em que a largura de banda ou o espaço de armazenamento são limitados, ou quando é desejável reduzir a complexidade computacional em algoritmos de processamento de dados.
Para entender o escrito acima, consideremos o seguinte exemplo, adaptado e estendido da documentação do NumPy.
- São conhecidos 200 pontos, que correspondem a valores de pesos e alturas para atletas de 4 modalidades: basquete, futebol americano, ginástica e maratona.
- Um novo ponto é fornecido, para o qual se deseja saber a provável modalidade do atleta correspondente.
Vamos começar visualizando a situação inicial, os 200 pontos. Para esta simulação de pontos, usaremos o método make_blobs do Scikit-Learn.
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from matplotlib.colors import from_levels_and_colors
import matplotlib.image as image
from PIL import Image
from numpy import arange
# definindo o estilo do gráfico e as cores
plt.style.use("seaborn-v0_8-muted")
prop_cycle = plt.rcParams["axes.prop_cycle"]
colors = prop_cycle.by_key()["color"]
# criando os clusters para as classes
classes = ["Basketball", "Football", "Gymnast", "Marathon"]
X, y_true, centers = make_blobs(
n_samples=200,
centers=((102, 203), (132, 193), (45, 155), (57, 173)), # centroides de partida
cluster_std=3.5,
random_state=0,
shuffle=False,
return_centers=True,
)
# criando o gráfico
fig, ax = plt.subplots()
with Image.open("images/CP_banner_transp.png") as logo:
logo_width, logo_height = logo.size
axin = ax.inset_axes([100,140,45,15], transform=ax.transData)
axin.imshow(logo)
axin.axis('off')
cmap, norm = from_levels_and_colors(arange(0, y_true.max() + 2), colors[: len(classes)])
scatter = ax.scatter(X[:, 0], X[:, 1], c=y_true, cmap=cmap, norm=norm)
ax.legend(handles=scatter.legend_elements()[0], labels=classes)
ax.set_xlabel("Weight / kg")
ax.set_ylabel("Heigth / cm")
ax.set_title("Height vs weight for 4 athlete classes")
plt.show() Veja no gráfico acima que já destacamos as quatro classes de atletas. Esta classificação pode ser feita com um algoritmo do tipo K-means, que tenta separar amostras em grupos de igual variância minimizando a soma dos quadrados dentro de um determinado cluster.
Com os clusters criados, podemos resumi-los a partir de seus centroides. Então, dado um novo ponto, que chamaremos de observation (observação, como se fosse um ponto experimental), podemos atribuí-lo a um dado cluster a partir da menor distância entre este novo ponto e o centro de cada centroide. Veja que estamos descrevendo exatamente uma quantização vetorial, com a criação dos clusters, seus centroides e menor distância ao centroide. Comecemos incrementando nossa visualização com os centroides, nosso ponto que desejamos classificar e os vetores de distância:
from numpy import tile, sqrt, sum
fig, ax = plt.subplots()
# criando o gráfico de clusters, destacando o centro de cada um com um círculo preto
base_scatter = ax.scatter(X[:, 0], X[:, 1], c=y_true, cmap=cmap, norm=norm)
# os centros são os símbolos de quantização de nosso exemplo e foram estipulados na
# célula anterior, manualmente, como início de nossa simulação
centers_scatter = ax.scatter(
centers[:, 0],
centers[:, 1],
c=["black"] * len(centers),
s=200,
alpha=0.5,
label="Centers",
)
# criando um quadrado vermelho para destacar nosso atleta a ser classificado
observation = array((111, 188))
observation_scatter = ax.scatter(
*observation, c=["red"], marker="s", s=150, label="Observation", zorder=2
)
# fazendo a conta de distância de cada centro de cluster ao nosso atleta
origin = tile(observation, (4, 1))
diff = centers - observation
dist = sqrt(sum(diff**2, axis=1))
# criando vetores para representar as distâncias
distance_vectors = ax.quiver(
origin[:, 0],
origin[:, 1],
diff[:, 0],
diff[:, 1],
units="xy",
angles="xy",
scale_units="xy",
scale=1,
color=colors,
linewidth=0.5,
edgecolor="black",
)
# terminando o gráfico com a legenda, os rótulos dos eixos e os títulos
handles = base_scatter.legend_elements()[0] + ax.get_legend_handles_labels()[0]
labels = classes + ax.get_legend_handles_labels()[1]
ax.legend(handles=handles, labels=labels)
ax.set_xlabel("Weight / kg")
ax.set_ylabel("Height / cm")
ax.set_title(
"Arrows show distance from observation (athlete to be classified)", fontsize=10
)
fig.suptitle("Height vs weight for 4 athlete classes")
with Image.open("images/CP_banner_transp.png") as logo:
logo_width, logo_height = logo.size
axin = ax.inset_axes([100,140,45,15], transform=ax.transData)
axin.imshow(logo)
axin.axis('off')
plt.show() Como o vetor de menor comprimento é o que une nosso ponto ao centroide do cluster de jogadores de basquete, temos, então, que provavelmente este ponto simboliza um jogador de basquete. Simples a ideia, certo?
Mas onde está o broadcasting aqui?
No código, criamos uma simulação a partir de valores dos centros dos clusters, centroides, cujos valores são:
centersarray([[102, 203],
[132, 193],
[ 45, 155],
[ 57, 173]])
Posteriormente, acrescentamos o ponto que desejamos classificar:
observationarray([111, 188])
Veja que os dois arrays tem dimensões distintas. Mas o cálculo de distância passa, primeiro, pela diferença entre estes dois arrays. Logo, houve um broadcasting nesta operação. O valor da diferença foi armazenado na variável diff segundo o código anteriormente mostrado:
diffarray([[ -9, 15],
[ 21, 5],
[-66, -33],
[-54, -15]])
Vamos entender o porquê a conta é possível com base nas regras de broadcasting:
tabela_broadcasting(
("centers", "observation", "diff"), (centers, observation, diff), (12, 5, 6, 4)
) array | ndim | shape | size
------------ | ----- | ------ | ----
centers | 2 | (4, 2) | 8
observation | 1 | (2,) | 2
diff | 2 | (4, 2) | 8
- os arrays iniciais são centers e observation
- as dimensões são 2 e 1, respectivamente
- a dimensão mais à direita de ambos tem tamanho 2, sendo iguais, permitindo broadcasting
- a próxima dimensão, seguindo para a esquerda, em centers é 2 e em observation é 1 (por ausência), permitindo broadcasting
- o array resultante diff tem dimensão 2 (maior entre os arrays iniciais), com tamanhos (4, 2), igual ao array centers (maior dentre os iniciais)
Por fim, a distância em si do ponto para cada centroide é dada pela raiz da soma dos quadrados das diferenças e tais distâncias foram associadas à variável dist no código:
for class_, distance in zip(classes, dist):
print(f"Classe: {class_:^11}| Distância: {distance:.2f}")Classe: Basketball | Distância: 17.49 Classe: Football | Distância: 21.59 Classe: Gymnast | Distância: 73.79 Classe: Marathon | Distância: 56.04
Novamente, como a menor distância é para o centroide da classe de jogadores de basquete, classificamos o atleta como jogador de basquete.
Com esse exemplo, temos a ideia básica de quantização vetorial e como ela se relaciona com o broadcasting do NumPy quando este é utilizado neste contexto. Em breve devo abordar compressão de imagens e de sinais em artigos aqui do site, que por baixo aplicam a mesma ideia deste exemplo.
Conclusão
Neste artigo, revisitamos o conceito de array e vimos como o broadcasting do NumPy facilita significativamente operações matemáticas com arrays. Vimos como o broadcasting atua em um exemplo de quantização vetorial.
O que mais de NumPy gostaria de aprender com exemplos práticos aqui no site? Deixe nos comentários.
Para mais artigos relacionados, confira a tag NumPy.
Até a próxima!




